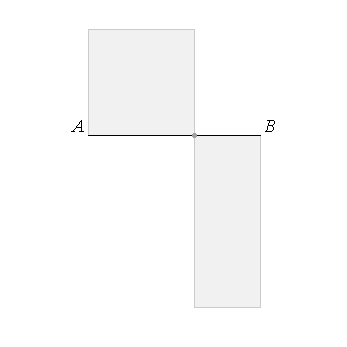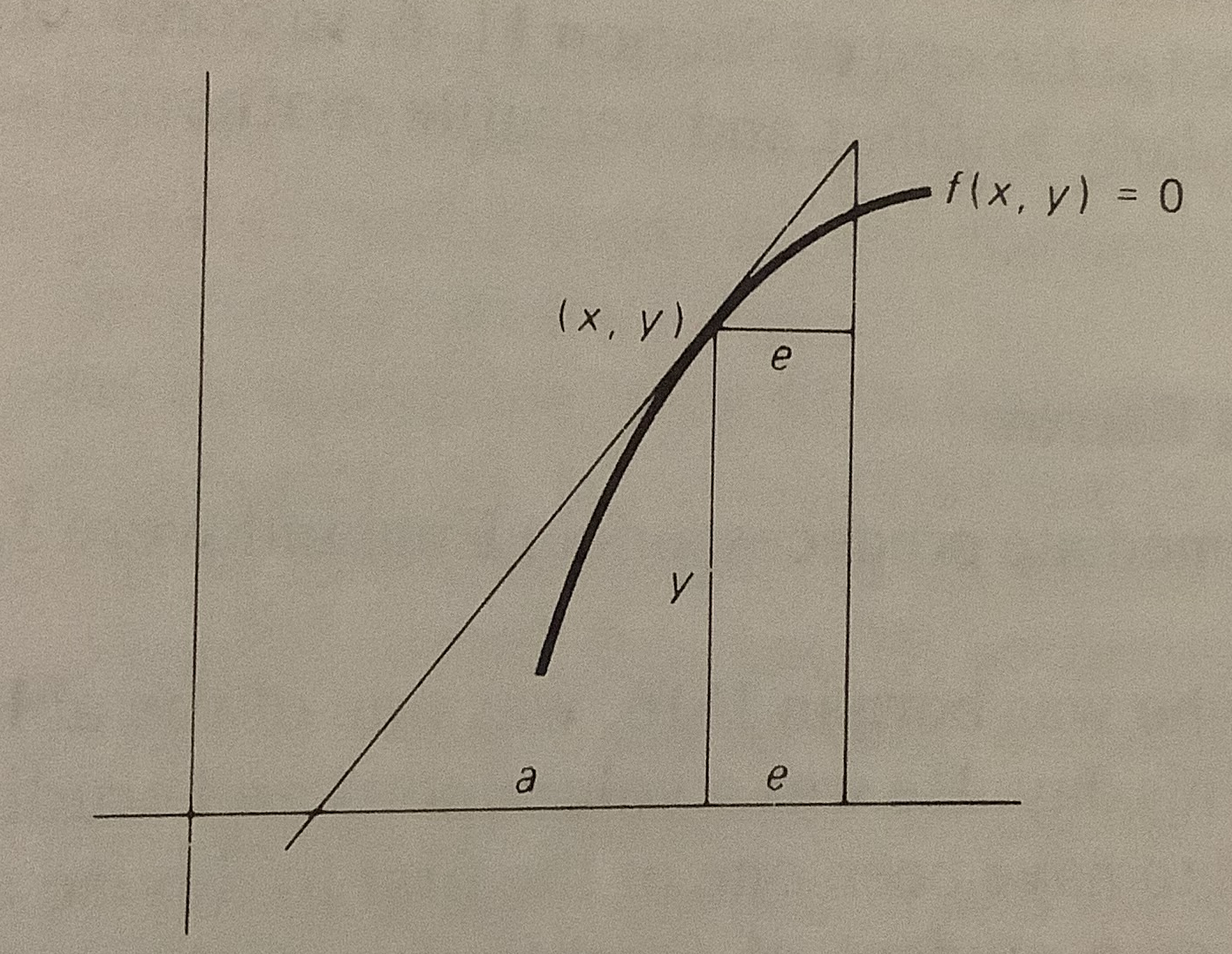Math History Notes
Day 1
Welcome to class!
- Welcome to the July term!
- I’m very glad you’re here.
Course overview
About us
(Usually) Mostly a class for future teachers
- Name
- Major
- Why teach math? (if future teacher, if not, why this class?)
- What is goal in this class?
- Random fact.
- Name: John Hammond
- Major: Undergrad BSEd, lots of computer science (Missouri State 🧸), MA Math (Mizzou 🐯)
- Why teach math? Brief story.
- What is goal in this class? Help foster an appreciation of mathematics
- Random fact Wombats poop cubes.
- Name
- Major
- Why teach math? (if future teacher, if not, why this class?)
- What is goal in this class?
- Random fact.
Now about your thoughts on math:
I asked over email last week the following questions:
- What do you think that math is? If someone asks, “what is math?” what would you say?
- What is your favorite topic in mathematics? Such as favorite subject, favorite lesson, favorite fact, etc.
- What is your goal for the class? Such as “at the end of the semester, I hope __”
Blackboard highlights
You’ve already had access for a few days. We’ll talk highlights.
Syllabus quick overview.
We’ll talk highlights.
You probably have lots of questions…
… questions?
A note about course ordering
- Sketches discuss individual concepts at a time
- We’ll be visiting many different cultures/countries in many different time periods
- This will mean having to remind yourself of what time you’re considering
- … it’s not difficult, just worth noting
- Also, the order of the sketches is out-of-order to the textbook it to paint a narrative of my choosing, putting together some interconnected themes.
Let’s do a little class!
Why math?
- Economics / Trade
- Religion
- Bureaucracy - Taxes, Armies,
- Calendars
Number Systems (previewing Sketch 1)
Different cultures use(d) different bases and number systems
- Aztecs, Mayans* (base 20—vigesimal)
- Incans, Indians (base 10—decimal)
- Mesopotamians (e.g. Babylonians) (base 60—sexagesimal)
How do we see numbers in different bases?
Pick a base \(b\), then you can represent any number, \(N\), uniquely by: \[N = a_n b^n + a_{n-1}b^{n-1} + \dots + a_1 b + a_0\]
For example, in base 10, \[6735 = 6\cdot 10^3 + 7\cdot 10^2 + 3 \cdot 10 + 5\]
- If we want base 2, the number \(13 = 1\cdot 2^3 + 1\cdot 2^2 + 1\), we write: \[13_{ten} = 1101_{two} = 1101_{2}\]
- Let’s convert into different bases to practice:
- 782 to base 60
- 782 to base 20
Positional vs. not positional.
- What do you think these terms mean for number system?
- Can you give an example?
Day 2
Sketch 1: Keeping Count: Writing Whole Numbers
Discussing the homework questions
Another Meso-American Way of Representing Number
The Inca Empire
- Where: Peru, Bolivia, Chile, Ecuador, Argentina
- Height of the empire in 15th century ~ 6 million people
Life and Math in the Inca Empire
- “Postal System” of runners (300 miles in 24 hours!)
- Decimal number system
- No (known) written language
- Number data recorded and transmitted with the quipu, a string of
knotted colored cords
- number of knots represents digits according to (Ifrah, 1985)
- Here are some sample drawings from that author
- Quipu keepers in urban areas prepared, read, and stored quipu records
for the government.
 3
3
Quipu and an abacus
Drawing by Felipe Guaman Poma de Ayala of the Chief Accountant in Nueva corónica y buen gobierno (New Chronicle and Good Government) in 1615
 (Guaman, n.d.)
“Chief accountant and treasurer, Tawantin Suyu khipuq kuraka, authority in charge of the knotted strings, or khipu, of the kingdom”
(Guaman, n.d.)
“Chief accountant and treasurer, Tawantin Suyu khipuq kuraka, authority in charge of the knotted strings, or khipu, of the kingdom”
… by the way, the whole book is available online here!
Inca Abacus Worksheet
- Really long walk through
- Counting Beads (small objects)
- Sheet for a yupana
“Nutshell” pages 5-25
Egyptian Arithmetic
Try the following multiplication and division problems using the Egyptian system of “doubling-and-halving”:
- 57 * 63
- 364 * 28
- 181 ÷ 12
- 213 ÷ 13
The Rhind (Ahmes/Ahmose) Papyrus
- Ahmes was an Egyptian scribe, born about 1680 B.C.
- Wrote the papyrus
- … says he copied from earlier work circa 2000 B.C.
- The papyrus contains math:
- division tables,
- problems of area and volume,
- methods for solving various types of problems and equations.
- Purchased in 1858 by Alexander Henry Rhind.
- Original likely 18 feet by 13 inches
- Rhind’s fragment partial;
- rest found in New York Historical Society
Quote from Burton’s History of Mathematics (Burton, 2011)
The Rhind Papyrus starts with a bold premise. Its content has to do with “a thorough study of all things, insight into all that exists, knowledge of all obscure secrets.” It soon becomes apparent that we are dealing with a practical handbook of mathematical exercises, and the only “secrets” are how to multiply and divide.
 5
View a full-size scrollable version on the British Museum Website
5
View a full-size scrollable version on the British Museum Website
Translation of Cuneiform:
- Story of Darius I defeating a revolt in Persia in 516BC
- Carved on Bisotun Cliff in Iran
- four-hundred feet above the ground
Written in Old Persian (Elamitic), Babylonian, and Persian
# - (side note) Why are our numbers called Hindu-Arabic?7 :
- Translated in 1846 by Henry Rawlinson
Evolution from Indian numerals to modern Hindu-Arabic numerals
- A common chart you’ll see in many texts such as (Eves, 1990; Katz, 2009):
- Let’s do better, with charts from Georges Ifrah (Ifrah, 1985, pp. 485–489)
- (and remember to share his story)
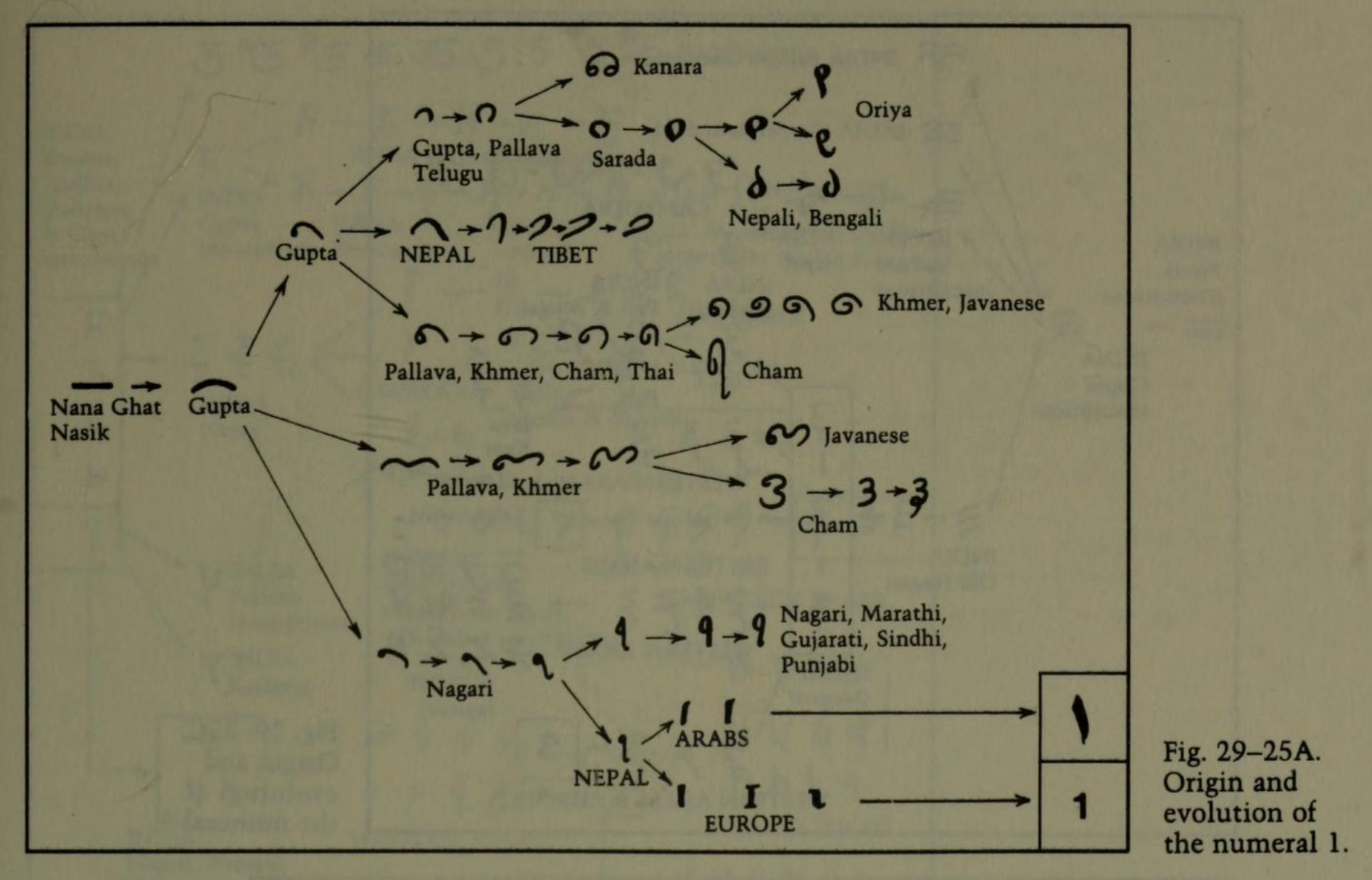
Hindu-Arabic vs Arab-Hindi numerals
- Not everyone uses the Hindu-Arabic numerals
- Not even everyone in Eastern Arab or some Indian regions.
- Eastern Arabic numerals or the Arabic-Hindu numerals and the very similar Urdu numbers 8
| Modern Hindu-Arabic | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Modern Eastern Arabic | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ | ١٠ |
| Urdu | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | ۱۰ |
How did the “Hindic” form of the numbers evolve? Looking at first five numbers (Ifrah, 2000, p. 467):
# 
Day 3
Sketch 2: Reading and Writing Arithmetic: The Basic Symbols
Discussing the homework questions
Sketch 4: Broken Numbers: Writing Fractions
Egyptian Fractions and Arithmetic
- Unit fractions, and special symbols fractions
- Example: Write 5/6 as an Egyptian fraction.
- Example: Double 1 1/15
- On the back is the “\(2/n\) table”
- Some examples:
| n | 2/n |
|---|---|
| 5 | 3 15 |
| 7 | 4 28 |
| 9 | 6 18 |
| 11 | 6 66 |
| 13 | 8 52 104 |
| … | … |
| 61 | 40 244 488 610 |
| … | … |
An Exercise from the Ahmes (Rhind) Papyrus
- How do you divide 9 loaves of bread between 10 men?
- Our way: 9 ÷ 10 = 9/10 of a loaf per man
- Mathematically, this is fair, but the guy with 10 tenths is probably not too happy!
The Ahmes Bread Problem
- The Egyptian way:
- 9 ÷ 10 = 2/3 + 1/5 +1/30
- The nine loaves of bread seem to be more “fairly” distributed this way!
Mesopotamian Fractions
An article search aside…
- Let’s say I’m looking for a particular article on reciprocal table.
- Got here: https://www.degruyter.com/document/doi/10.1515/za-2016-0016/html Darn! $42????
- To the library! (Copy the DOI or other information)
- No article. Darn again!
- Toggle switch. Hooray!
- Now it’s open, we can scroll through and see the tablet
Mesopotamian Fractions
- They avoided using fractions like 1/7 (why?)
- Let’s do the division in base 60 and see!
- Estimating fractions with denominators that are not factors of 60
- Reciprocal table:
| \(n\) | \(n^{-1}\) |
|---|---|
| 2 | 30 |
| 3 | 20 |
| 4 | 15 |
| \(\dots\) | |
| 1,20 | 45 |
| 1,21 | 44,26,40 |
- Remember we have to determine number “place”
Simon Stevin and Symbolism
- 1548-1620 (modern Belgium), wrote in Dutch
Decimal Fractions (in Europe)
- Published De Thiende (’The Tenth’) in 1585
- You can find it here (a 1606 English edition) (Stevin, 1608)
Operationswith decimals; circle-number notation for place value
- (me: do an example specifically, and also look at the link above)
- … Napier would use decimals in his work on logarithms soon after
- Published De Thiende (’The Tenth’) in 1585
Day 4
Sketch 12: A Cheerful Fact: The Pythagorean Theorem
A Mesopotamian question:
A translation of a Babylonian tablet which is preserved in the British museum goes as follows:
4 is the length and 5 the diagonal. What is the breadth ? Its size is not known. 4 times 4 is 16. 5 times 5 is 25. You take 16 from 25 and there remains 9. What times what shall I take in order to get 9 ? 3 times 3 is 9. 3 is the breadth.
Plimpton 322
- Plimpton 322
- Plimpton 322

Figure 1: Numeric translation in (Eves, 1990)
- Seemingly unrelated fact:
- Seemingly unrelated fact:
- Back to Plimpton

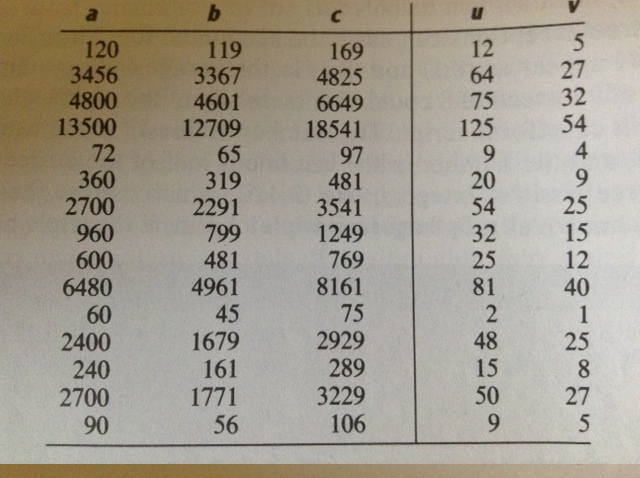
Tables from (Eves, 1990, pp. 45, 46)
- Seems plausible: the numbers \(u\) and \(v\) (and so \(a=2uv\)) of the form \(n=2^a 3^b 5^c\) for non-negative integers \(a, b,c\)
- Back to Plimpton
- Back to Plimpton
- What about column 4?
- Entries in column 4 correspond to \((c/a)^2\).
- What is \(c/a\) for a general right triangle?
- the secant of a base angle
- Going down the table, (Eves, 1990) points out the value “decreases by almost exactly 1/60 as we pass from one line of the table to the next, and the corresponding angle decreases from \(45^\circ\) to \(31^\circ\).”
- We have a secant table! in 1800BCish.
- Plimpton 322 - Counter Views
- First - Sherlock Holmes in Babylon (Buck, 1980)
- Fascinating case
- Mysterious clues
- Eleanor Robson - Neither Sherlock Holmes Nor Babylon (Robson, 2001)
- Not Sherlock Holmes:
- Math is written by people
- We need to view in historical setting
- Not just “cherry-pick the ‘cleverest’ or ‘most-sophisticated’ mathematical procedures”.
- Can’t just deduce like a locked room mystery
- :-(
- Math is written by people
- First - Sherlock Holmes in Babylon (Buck, 1980)
- Plimpton 322 - Counter Views
- Nor Babylon:
- The tablet is from 60 years before Hammarabi takes Babylon and creates Babylonia - … though this is a pedantic argument of the original author’s creative choice of words…
- Argues against Pythagorean triples
- Very against the trig table
- No record of use of angle measurement
- In favor of a table of reciprocals
- Nor Babylon:
- Plimpton 322 - Pro Views
- The most recent work is August 2017 (Mansfield & Wildberger, 2017)
- argues that it is an exact ratio-based trig table
- no reliance on angles.
- … due to use of base 60, no need to approximate fractions
- The most recent work is August 2017 (Mansfield & Wildberger, 2017)
Chinese(?) Pythagorean Theorem
In the Zhoubi Suanjing (translated The Arithmetic Classic of the Gnomon and the Circular Paths of Heaven)
Here is a photo of a Ming dynasty 1603 copy:

And here is a more modern focused image

- This is functionally similar to Thabit Ibn Qurra’s proof without words mentioned in (Berlinghoff & Gouvêa, 2015)
- (Chemla, 2005) notes that the two proofs are distinct in the manner of the interpretation of the diagrams.
- Thabit physically moves the pieces to construct two ’unequal squares’
- Liu Hui (commenting on the Zhou work) viewed it as two different ways to construct the same physical area (note that the external triangles are likely a drawing aid and not used in the proof, according to Chemla)
- (Chemla, 2005) notes that the two proofs are distinct in the manner of the interpretation of the diagrams.
- As an aside, (Eves, 1972) attributes this to Bhaskara; I haven’t traced that down further.
- Let’s take a look at the proof Head to Geogebra!
Pythagorean Number Theory
- Pythagoreans loved numbers!
- Special number properties (composite numbers)
- Pythagorean triples (from Mesopotamia?)
- Triangular, square, pentagonal, etc. numbers
- “Perfect” numbers (along with “Deficient” and “Abundant” numbers)
- “Amicable”/“Friendly” numbers11
- Sum of odd numbers
(Opposite of) a homework question, did you notice the sum of odd numbers?
- Examples of Figurate Numbers
- Triangular Numbers: \(1, 3, 6, 10, 15, 21, \dots\)
- The third triangular number, denoted \(T_3\), is 6.
- Square Numbers: \(1, 4, 9, 16, 25, \dots\)
- The fourth square number, \(S_4\), is 16.
- Pentagonal numbers: \(1, 5, 12, 22, 35, \dots\)
- The second pentagonal number, \(P_2\), is 5
- Triangular Numbers: \(1, 3, 6, 10, 15, 21, \dots\)
- Figurate number relations
- Square in terms of triangular numbers
- Square in terms of “gnomons”
- from Pythagoras, according to Proclus (Heath, 1921):
- Take a square number that is odd
- Add this to the square which is the sum of all preceding odd numbers.
- This makes the square of all odd numbers up to the original
- \(m^2 + \left( \dfrac{m^2 -1}{2} \right)^2 = \left(\dfrac{m^2 +1}{2}\right)^2\)
- Pentagonal numbers in terms of squares and triangles
- Perfect, Abundant, Deficient
- First, we need to be comfortable with finding divisors:
- What are the divisors of: 6? 18? 28? 39?
- Proper divisors are those divisors which are not equal to the number itself.
- A perfect number one that equals the sum of its proper divisors.
- After we talk about Euclid, we might come back to this. It’s remarkable!
- An abundant number is one such that the sum of the proper divisors is greater than the number.
- A deficient number is one such that the sum of the proper divisors is less than the number.
- First, we need to be comfortable with finding divisors:
- Amicable Numbers
- What are the proper divisors of 220 and 284?
- 220:
- 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110
- 284:
- 1, 2, 4, 71 and 142
- What neat thing do you observe?
Day 5
Sketch 7: Measuring the Circle: The story of \(\pi\)
How many digits do we want/need?
- Our reading discusses level of accuracy
- According to (Edu, 2016), NASA uses 3.141592653589793
In the article, they note that where Voyager 1 was at the time, 12.5 billion miles from earth, if they used this number
“It turns out that our calculated circumference of the 25 billion mile diameter circle would be wrong by 1.5 inches.”
Three classic problems:
With just a compass and unmarked straight-edge
- trisect an angle
- duplicate the cube
- square the circle
What does it mean to “square” something?
- Let’s find the areas of rectangles and triangles! (to Geogebra!)
Egyptian approximation - a setup and an assignment
Here’s an activity to try to see where \(A = (8/9 d)^2\) for the area of a circle might come from
- Show by experiment (using pennies, for example), that a circle of diameter 9 can essentially be filled by 64 circles of diameter 1.
- (Begin with one penny in the center, surround it with a circle of 6 pennies, and so on).
Use the fact that 64 circles of diameter 1 also fill a square of side 8 to show how the Egyptians may have derived their formula for the area of a circle, \(A=(8/9d)^2\) where \(d\) is the diameter of the circle.
Note that \(\pi\) isn’t a constant Egyptians used, though, per (Imhausen, 2008):
Egyptians did not use \(\pi\). As can be seen from the symbolic representation of the text, above, the constant used to calculate the area of a circle was \(\frac19\), which was clearly not an extremely bad approximation of \(\pi\) , but rather the constant appropriate to the Egyptian method of mathematizing circles.
Hippocrates: Quest to Square the Circle
- What do we mean by “squaring”?
- 450 B.C. Hippocrates finds the area of a curved figure called a lune (crescent moon shape).
- First non-rectilinear area calculation
- The Geogebra activity!
Archimedes and double exhaustion
- Inscribing and circumscribing polygons in/around a circle
- Compare the perimeter of the polygon with diameter of circle
- Since perimeter is close to circumference of the circle:
- \(\dfrac{\text{perimeter}}{\text{diameter}} \approx \dfrac{\text{circumference}}{\text{diameter}} = \pi\)
- inscribed polygon will be lesser
- circumscribed with be greater
- Gives as good an approximation as you could want
- Here’s a Geogebra demo
Archimedes’ Other works and The Method
- Born in Syracuse 287 B.C. on the island of Sicily.
- Unlike any other ancients we’ve discussed so far, we know relatively a lot.
- Figures prominently in Plutarch’s Lives of the Noble Grecians and Romans (1st century AD)
- Archimedes also writes prefaces for each book
- On Floating Bodies
- On the Equilibrium of Planes
- Quadrature of the Parabola
- On the Measurement of the Circle
- On the Sphere and Cylinder
- On Spirals
- The Method
The Method
From (Gould, 1955) (NOTE TO SELF: Don’t advance the slide)

Figure 2: Archimedes Sphere Construction

Figure 1: Archimedes Sphere Construction
First use of \(\pi\)
- William Jones in 1706 wrote Synpsis Palmoariorum Matheseos or A New Introduction to the Mathematics
- “In a short and Easie Method” … “Design’d for the Benefit, and adapted to the Capacities of BEGINNERS”
- Here’s the book (Jones, 1706)
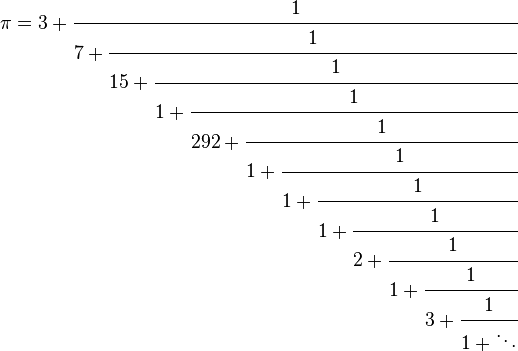
More different expressions of \(\pi\).
We saw various fractions to represent \(\pi\).
- What about infinite fractions
- Let’s talk about continued fractions.
- Term was first used by John Wallis in 1695
- idea is older

Sketch 8: The Cossic Art: Writing Algebra with Symbols
Discussing reading and problems
If we wish, visit Florian Cajori’s History of Mathematican Notations (1927)
An early Greek example
- First, the number system:
- Alphabetical numbers
- Diophantus Introduces symbolism to mathematics
- Diophantus’ Subtraction Symbol: Probably from the Greek word for “lacking” : leipis or \(\lambda\epsilon\iota\psi\iota\varsigma\) - symbolized as \(\not\Lambda\) (note this is the best I can typeset it… bar through capital lambda)
- Diophantus’ Symbolism
- unit: “monades” \(\stackrel{\circ}{M}\)
- “number” (the unknown): “arithmos” \(\varsigma\)
- “squares” (number multiplied by itself) \(\Delta^\Upsilon\) “dynamis”
- “cubes” (square multiplied by its side) \(K^\Upsilon\) “kubos”
- “square-squares” (square multiplied by itself) \(\Delta \Delta^\Upsilon\) “dynamo-dynamis”
- “square-cubes” (squares multiplied by cubes having same side) \(\Delta K^\Upsilon\) “dynamo-kubos”
- “cube-cubes” (cube multiplied itself) \(K K^\Upsilon\) “kubo-kubos”
- Examples (write in our modern notation):
- \(K^\Upsilon \alpha \Delta^\Upsilon \iota \gamma \varsigma \epsilon\)
- \(K^\Upsilon \alpha \varsigma \eta \not\Lambda \Delta^\Upsilon \epsilon \stackrel{\circ}{M} \alpha\)
Sketch 9: Linear Thinking: Solving First Degree Equations
Basic solving of first degree equations is basic
- Berlinghoff and Gouvea write: “Because solving linear equations is relatively easy, few standard history books have sections specifically on that subject.”
- We’ll take a look at linear equations, and
- things that are linear adjacent
Egyptian linear algebra: Single and Double False Position
- False Position Example 1
Ahmes Papyrus, problem 26: A quantity; its fourth is added to it. It becomes 15.
- x + (1/4)x = 15
- Guess \(x=4\).
- 4 + (1/4)(4) = 4+1 = 5
- 15/5 = 3
- 4 x 3 = 12
- False Position Example 2
A quantity; its third and its fifth are added to it. It becomes 46.
- x + (1/3)x + (1/5)x = 46
- Guess \(x=15\).
- 15 + 5 + 3 = 23
- 46/23 = 2
- 15 x 2 = 30
- Double False Position (another example)
From Daboll’s Schoolmasters’ Assistant 1837 quoted in (Bunt et al., 1988)
A, B, and C built a house which cost $500, of which A paid a certain sum; B paid 10 dollars more than A and C paid as much as A and B both; how much did each man pay?
Process:
- Guess
- Find error
- Repeat
- Cross-multiply guesses and errors
- Take the difference (if same sign) or the sum (if different)
- Here I mean subtract the whole numbers or add the whole numbers (signless)
- Divide by the difference/sum of the errors
- Answer.
- A final… er… questionable question
Cited in (Bunt et al., 1988) from The American Tutor’s Asistant 1817
When first the marriage know was ty’d
Between my wife and me,
My age was to that of my bride
As three times three to three
But now when ten and half ten years,
We man and wife have been,
Her age to mine exactly bears,
As eight is to sixteen;
Now tell, I pray, from what I’ve said,
What were our ages when we wed?Let’s solve it (one more click reveals answer)
Thy age when marry’d must had been Just forty-five; thy wife’s fifteen
Ew.
Linear Systems in Mesopotamia
- A first example of a linear system
From VAT 8389:
 [fn: https://primeviridian.blogspot.com/2015/03/ancient-babylonian-mathematics-tablet.html]
[fn: https://primeviridian.blogspot.com/2015/03/ancient-babylonian-mathematics-tablet.html]
Solving a system of two equations and two unknowns. As quoted in Katz (Katz, 2003)
from the Old Babylonian text VAT 8389: One of two fields yields 2/3 sila per sar, the second yields 1/2 sila per sar (sila and sar are measures for capacity and area, respectively). The yield of the first field was 500 sila more than that of the second; the areas of the two fields were together 1800 sar. How large is each field?
- Write this in modern notation
- How would you solve it?
- The scribe’s solution:
- \(x = y = 900\).
- \(2/3 \cdot 900 - 1/2 \cdot 900 = 150\)
- … off by 350!
- Multiply 350 by \(6/7\) to find 300.
- Answer: \(x=900+300=1200\) and \(y=900-300=600\).
- Why \(6/7\)?
- \(2/3 (1) - 1/2(-1) = 7/6\),
- … so each increase of \(x\) increases the output by \(7/6\).
- What increase, \(s\), should we do for \(x\)?
- \(7/6s = 350\) or \(s= 300\).
Another Mesopotamian (non-linear) system
The AO 8862 tablet
- old tablet - 1700’s BC.
- square prism with problems on four sides
- currently held at the Louvre
 [fn: http://ressources.louvrelens.fr/EXPLOITATION/oeuvre-ao-8862.aspx]
[fn: http://ressources.louvrelens.fr/EXPLOITATION/oeuvre-ao-8862.aspx]
Quoted in (Bunt et al., 1988)
Length, width. Length and width I have multiplied and thus formed the area. I have further added the excess of the length over the width to the area: 3,3. Further, I have added the length and width: 27. Required: length, width, and area.
- (pick some variables and talk, I give it away on the next line:)
- \(xy + y - x = 3,3\) and \(x + y = 27\).
The scribe’s solution:
- (Given) 27 and 3,3, the sums
- (Result) 15 length, 12 width, 3,0 area.
- You follow this method:
- 27 + 3,3 = 3,30
- 2 + 27 = 29
- Take half the 29 (14;30)
- 14;30 \(\times\) 14;30 = 3,30;15
- 3,30;15 - 3,30 = 0;15
- 0;15 has 0;30 as square root
(continued)
- 0;15 has 0;30 as square root
- 14;30 + 0;30 = 15 length.
- 14;30 - 0;30 = 14 width.
- Subtract the 2 you added to 27 from 14, the width:
- 12, the real width
- 15, length, 12, width; I have multiplied
- 15 \(\times\) 12 = 3,0 area
- 15 - 12 = 3
- 3,0 + 3 = 3,3
Indian Linear Proportions - The Rule of Three
- Āryabhaṭa (born 476 AD) writes Āryabhaṭīya when he is 23
- The Āryabhaṭīya is an astronomical book
- The earliest existing work in Indian mathematics
- he dates the manuscript and says how old he is.
As translated in (Clark, 1930), he thinks well of himself:
By the grace of God the precious sunken jewel of true knowledge has been rescued by me, by means of the boat of my own knowledge, from the ocean which consists of true and false knowledge.
- The math chapter is expanded and explained by Bhāskara I
- Written in verse (sutras) with puns as memory devices
The Rule of Three: Āryabhaṭa writes: (Keller, 2006)
Now, when one has multiplied that fruit quantity in the Rule of Three by the desire quantity
What has been obtained from that divided by the measure should be this fruit of the desire
The denominators are respectively multiplied to the multipliers and the divisor.
- Huh???
Bhaskara clarifies: (Keller, 2006)
In order to bring about a Rule of Three the wise should know that in the dispositions
The two similar quantities are at the beginning and the end. The dissimilar quantity is in the middle.- physically arrange, like one a table;
- two right numbers are multiplied. The left divides that result.
Here’s an example from Bhaskara (Keller, 2006)
A lot of cattle is said to be made of eight tamed, three to be tamed.
Out of one thousand and one, how many have been tames and how many are the others?
- This time, to get “similars” we need total collection of cows; 8+3=11 in the lot; 1001 in total:
- Write similars on outside, dissimilar inside:
- Tamed and untamed 11; tamed 8; total 1001
- Multiply the two right numbers and divide by the left number.
- 725; units? Tamed! (the units of the middle)
- So there are 1001-725 = 273 untamed.
One more example? Merchants and earnings! (Keller, 2006)
Merchants with respective investments of a half, a third and one eighth
have a profit of seventy minus one. What are their respective profits?
Here’s an example (Let’s make it up):
- Pick a number
- Pick a dollar amount
- Pick a thing you’d buy
- I bought NUMBER of THING YOU’D BUY for $ DOLLARS. How much THING YOU’D BUY can be obtained for $1?
- Write similars on outside, dissimilar inside:
- $ DOLLAR QUANTITY $1
- Multiply the two right numbers and divide by the left number.
- Answer!
- Contrast with an Egyptian “Rule of Three” problem
- Problem 72 of the Ahmes Papyrus (written about 2000 years before Āryabhaṭa)
written in modern phrasing, quoted in (Joseph, 2010)
100 loaves of pesu 10 are to be exchanged for a certain number of loaves of pesu 45. What is this certain number?
Note that pesu means weakness, so high pesu is lower quality bread.
- Find excess of 45 over 10; 35
- Divide 35 by 10; 3.5
- Multiply 3.5 by 100; 350
- Add 350 + 100; 450 is the answer
- Method suggests knowing \(\dfrac{y}{x} = \dfrac{g}{p} \equiv \dfrac{y-x}{x} = \dfrac{g-p}{p}\)
- Problem 72 of the Ahmes Papyrus (written about 2000 years before Āryabhaṭa)
Chinese Linear Systems
Jiuzhang suanshu or Nine Chapters on the Mathematical Art (around 200ish BC)
- Algorithms of finding square and cube roots
- Solutions to quadratic equations and systems
- Solutions of systems of up to five linear equations
- The method given is basically Gaussian Elimination
Example problem (Problem 1 of Chapter 8):
There are three types of grain. Three bundles of the best, plus two bundles of the second best, plus one bundle of the worst give a total of 39 units of flour. But two bundles of the best, plus three bundles of the second best, plus one bundle of the worst give a total of 34 units of flour. Finally, one bundle of the best, plus two bundles of the second best, plus three bundles of the worst give a total of 26 units of flour. How many units of flour can be made from one bundle (for each type of grain)?
Represented as columns in a table form:
\(\left(\begin{array}{ccc} 1 & 2 & 3 \\ 2 & 3 & 2 \\ 3 & 1 & 1 \\ 26 & 34 & 39 \end{array} \right)\)
… and do column-operations to reduce the matrix and solve the system.
Day 6
Day 7
Sketch 10: A Square and Things: Quadratic Equations
A Mesopotamian story problem:
Old Babylonian Story Problem ca. 1700 B.C, the solution to the question: “I have taken the area and two thirds of the side of my square and it is 0;35.”
Let’s work this one out.
You take 1 the “coefficient”. Two thirds of 1, the coefficient, is 0;40. Half of this, 0;20, you multiply by 0;20 (and the result) 0;6,40 you add to 0;35 and (the result) 0;41, 40 has 0;50 as its square root. 0;20, which you multiplied by itself, you subtract from 0;50 and 0;30 is the (side of) the square.”
al-Khwarizmi’s al-jabr
- Abu Ja’far Muhammad ibn Musa Al-Khwarizmi (c. A.D.780 - 850)
- Wrote on “algebra”, Hindu-Arabic numerals, spheres, and cones
- Worked as an astronomer and head librarian at the House of Wisdom under several caliphs
- Influential writings
- kitab al-jam’ wa’l-tafriq al-ḥisāb al-hindī (Book of Addition and Subtraction with Indian Numbers)
- original Arabic is lost, survived via Latin translations
- al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr wal-muqābala (Compendious Book on Calculaion by Completion and Balancing)
- Available here, 1831 translation (Rosen & Khuwarizmi, 1831)
- Provided algebraic proofs followed by geometric proofs.
- kitab al-jam’ wa’l-tafriq al-ḥisāb al-hindī (Book of Addition and Subtraction with Indian Numbers)
al-Khwarizmi
- al-jabra “restoration” – adding equal terms to both sides of an equation to remove negatives
- al-muqabala “reduction” – subtracting equal quantities from both sides
al-Khwarizmi
Using only positive numbers, he classified six types of quadratics “root” or “thing” refers to the variable, “number” is a constant.
- roots equal squares \(bx = ax^2\)
- roots equal numbers \(bx = c\)
- squares equal numbers: \(ax^2 = c\)
- squares and roots equal numbers: \(ax^2 + bx = c\)
- roots and numbers equal squares: \(bx + c = ax^2\)
- squares and numbers equal roots \(ax^2 + c = bx\)
al-Khwarizmi
(this was in our text as well) A problem and solution of al-Khwarizmi, as quoted in (Joseph, 2001, p. 477): “One square [mal] and 10 roots of the same equals 39 direhems.” Solution:
- You halve the “number” of roots: result 5.
- This you multiply by itself: result 25.
- Add this to 39: result 64
- Take the square root of this: result 8
- Subtract from 8 the result given in step 1: result 3.
- This is the root of the square you sought.
Another particular case of al-Kwharizmi: \(ax^2 + c = bx\)
- We follow a similar method
- But we can have more than one solution
- Or no solution.
- (Me) read the translation from (Lévy, 2002)
Algebra of Greece (Euclid)
:CUSTOMID: book-ii-of-elements
- Definition:
Any rectangular parallelogram is said to be contained by the two straight lines containing the right angle.
- Proposition II.1: (Bunt et al., 1988)
If there be two straight lines, one of which is divided into any number of parts, the rectangle contained by the two straight lines is equal to the rectangles contained by the divided line and the several parts of the divided line.
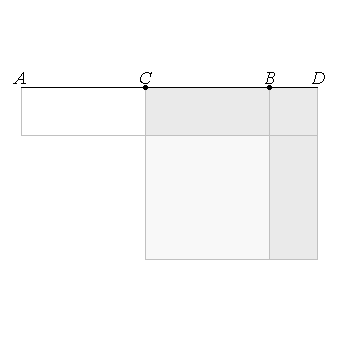
- Proposition II.4:
If a straight line be cut at random, the square on the whole is equal to the squares on the segments and twice the rectangle contained by the segments.
- Proposition II.5:
If a straight line be cut into equal and unequal segments, the rectangle contained by the unequal segments of the whole together with the square on the straight line between the points of section is equal to the square on the half.
(Here’s the algebraic construction pre-done) https://www.geogebra.org/m/jutayp4b
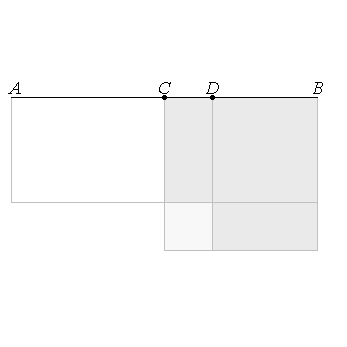
- Proposition II.6:
If a straight line be bisected and a straight line be added to it in a straight line, the rectangle contained by the whole with the added straight line and the added straight line together with the square on the half is equal to the square on the straight line made up of the half and the added straight line.
(Here’s the pre-done construction…) Here’s the construction on Geogebra
- Proposition II.11:
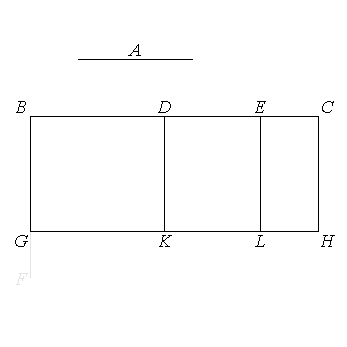
To cut a given straight line so that the rectangle contained by the whole and one of the segments is equal to the square on the remaining segment.
Let’s do the construction on Geogebra from scratch.
Day 8
TODO Sketch 5: Less than nothing?: Negative numbers
Sketch 28: Any Way You Slice It: Conic Sections
Omar Khayyam - Solutions to Cubics
- Khayyam discovered and extended a geometrical argument for solving cubics
- Leads to finding the real solution to cubic equations
- In Treatise on Demonstrations of Problems of al-jabra and
al-muqabala:
- “he emphasizes that the reader needs to be thoroughly familiar with the work of Euclid, Appolonius, and al-Khwarizmi in order to follow the solutions.” (Laubenbacher & Pengelley, 1999)
- Showed strong mastery of geometry
- Classification of solutions of some cubics (from (Joseph, 2001))
| Type | Method |
|---|---|
| \(x^3 = c\) | Intersection of two parabolas |
| \(x^3 + ax = c\) | Intersection of circle and parabola |
| \(x^3 \pm c = ax\) | Intersection of hyperbola and parabola |
| \(x^3 = ax + c\) | Intersection of two hyperbolas |
Sketch 11: Intrigue in Renaissance Italy: Solving Cubic Equations
The general solution to the cubic
- The people
- Antonio Maria Fior
- Student of Scipio Ferro
- Nicolo Fontana (1506-1557)
- Poor family
- two weeks of formal schooling
- self taught
- Taught math Venice, Verona, and Brescia
- Translated Euclid’s Elements among other works
- Called Nicolo Tartaglia
- French attack in 1512
- Disfigurement
- Tartaglia (the stammerer)
- Girolamo Cardano (1501 - 1576)
- well-educated
- medical doctor and mathematician
- Ludovico Ferrari (1522-1565)
- Poor family
- Came to work for Cardano
- Showed his brilliance
- Antonio Maria Fior
- The … math battles(?)
- Battles of science and mathematics
- Sample questions from Fior to Tartaglia (Nordgaard, 1938):
- “Find three numbers in triple proportion [x, 3x, 9x] such that if the square of the smallest is multiplied by the largest and the product be added to the mean number, the result is 7”
- “Find a number which added to twice its cube root gives 13”
- “Divide twenty into two parts such that one is the cube root of the other”
- …
- These are all forms of \(x^3 + mx = n\)
- Tartaglia defeats Fior.
- Goodbye Fior
- Please… please… please?
- Cardano wants Tartaglia’s solution.
- [Stage direction: Read from (Nordgaard, 1938)]
- Cardano wants Tartaglia’s solution.
- Let’s work through the poem.
Open (Gutman, 2005)
- Cardano finds another way
To solve \(x^3 + mx = n\), from Cardano’s Ars Magna, as quoted in (Dunham, 1991b):
Cube one-third the coefficient of \(x\); add to it the square of one-half the constant of the equation; and take the square root of the whole. You will duplicate [repeat] this, and to one of the two you add one-half the number you have already squared and from the other you subtract one-half the same… Then, subtracting the cube root of the first from the cube root of the second, the remainder which is left is the value of \(x\).
- Cardano’s Formula
If \(x^3 + mx = n\), then
\[x = \sqrt[3]{\frac{n}{2} + \sqrt{\frac{n^2}{4} + \frac{m^3}{27}}} - \sqrt[3]{-\frac{n}{2} + \sqrt{\frac{n^2}{4} + \frac{m^3}{27}}}\]
# - He didn’t write this (this is us translating)
- The different “types” of cubics
Cardano only dealt with positive quantities - negative numbers are still uncomfortable in the 16th century!
- Cube and first power equal to a number (what we did)
- Cube and number equal to first power
- Cube, square and first power equal to a number
- Cube equal to the square and first power
- …
- What about general cubics?
- Depressing a polynomial.
- Take \(ax^2 + bx + c = 0\)
- Substitute \(x = y - \frac{b}{2a}\) (Link to WolframAlpha).
- Observation?
- Take \(ax^3 + bx^2 + cx + d = 0\)
- Substitute \(x = y-\frac{b}{3a}\) (Link to WolframAlpha)
- Observation?
- Another Cardano example:
- Solve \(x^3 - 15x = 4\)
- Cardano’s formula: \(m = -15\), \(n=4\).
- …
- \(x=\sqrt[3]{2+\sqrt{-121}} - \sqrt[3]{-2+\sqrt{-121}}\)
- “But \(\sqrt{-121}\) is meaningless,” you say.
- This is casus irreducibilis
- \(\sqrt{-121}\) has no geometric meaning
- there is no square whose area is -121
- Let’s play for a moment, though:
- Cube \(2 + \sqrt{-1}\).
- \((2 + \sqrt{-1})^3 = 8 + 12\sqrt{-1} - 6 - \sqrt{-1}\)
- \(= 2 + 11\sqrt{-1}\)
- \(= 2 + \sqrt{-121}\)
- So \(\sqrt[3]{2 + \sqrt{-121}} = 2 + \sqrt{-1}\)
- Similarly, \(\sqrt[3]{-2 + \sqrt{-121}} = -2 + \sqrt{-1}\)
- So \(\sqrt[3]{2 + \sqrt{-121}} = 2 + \sqrt{-1}\)
- Similarly, \(\sqrt[3]{-2 + \sqrt{-121}} = -2 + \sqrt{-1}\)
- Coming back to Cardano’s solution to \(x^3- 15x = 4\)
- \(x=\sqrt[3]{2+\sqrt{-121}} - \sqrt[3]{-2+\sqrt{-121}}\)
- \(x=(2+\sqrt{-1}) - (-2 + \sqrt{-1})\)
- \(x=4\)
- So using \(\sqrt{-121}\) as an object gives a real solution.
- Mind-blow.
- Cardano called the solutions sophistic (from sophism meaning an argument designed to deceive)
- Ferrari solves the quartic
Cardano writes in Ars Magna (as recounted in (Dunham, 1991b)):
There is another rule, more noble than the preceding. It is Lodovico Ferrari’s, who gave it to me on my request. Through it we have all the solutions for equations of the fourth power.
General idea:
- Starting with a general quartic \[ax^4 + bx^3 + cx^2 + dx + e = 0\]
- Depress it using the substitution \(y=x-\frac{b}{4a}\), giving: \[y^4 + my^2 + ny = p\]
- Then cleverly introduce substitutions to turn it into a cubic.
- We can solve every cubic using Cardano’s method.
Day 9
Sketch 17: Impossible, Imaginary, Useful: Complex numbers
Another Cardano example:
We saw previously that \[ 4 = \sqrt[3]{2+\sqrt{-121}} - \sqrt[3]{-2+\sqrt{-121}} \] Here’s another example.
English translation (Cardano, 1993)
The second species of negative assumption involves the square root of a negative. I will give an example: If it should be said, Divide 10 into two parts the product of which is 30 or 40, it is clear that this case is impossible. Nevertheless, we will work thus…
- Head to Ars Magna chapter XXXVII, Rule II (in the Latin pdf, page 67)
- In the English translation by published by Dover, head to pg 219
Cardano concludes the discussion (Cardano, 1993, p. 220):
So progresses arithmetic subtlety the end of which, as is said, is as refined as it is useless.
Arithmetic of Rafael Bombelli
- Wrote l’Algebra in 1572
- Goal was to make algebra, inspired by Ars Magna, easier to understand
- He wrote that Cardano wasn’t clear (ma nel dire f’ oscuro) (van der Waerden, 1985)
- Include his newly discovered work by Diophantus
- He explained the solution to \(x^3 = 15x +4\), as quoted in
(van der Waerden, 1985)
- “At first, the thing seemed to me to be based more on sophism than on truth, but I searched until I found the proof”
- He was the first to observe that solutions with square roots of negatives appear in “conjugate pairs”
- he didn’t call it that, though
- Notation for \(\sqrt{-1}\), and rules to work with it:
- Our \(\sqrt{-1}\) is piú di meno and our \(-\sqrt{-1}\) is meno di meno
- Symbolically: R.q.0m.1 and m.R.q.0m.1
- This was the subject of chapter 2 of l’Algebra
From (Barrow-Green et al., 2019):
This will seem to be more artificial than real, and I held the same opinion myself, until I found the geometrical demonstration“ … Plus times plus of minus, makes plus of minus
Minus times plus of minus, makes minus of minus
Plus times minus of minus, makes minus of minus
Minus times minus of minus, makes plus of minus
Plus of minus times plus of minus, makes minus
Plus of minus times minus of minus, makes plus
Minus of minus times minus of minus, makes minus
- Chapter 1 is about computing radicals
- Quote about the particular topic, but gives the feel:
- (this is really fun - it illustrates how math’s a bit different today)
…In short, I shall set forth the method which is the most pleasing to me today and it will rest in men’s judgment to appraise what they see: meanwhile I shall continue my discourse going now to the discussion itself
Approximating radicals
Translation from (Arcavi & Bruckheimer, 1991):
Let us first assume that if we wish to find the approximate root of 13 that this will be 3 with 4 left over. This remainder should be divided by 6 (double the 3 given above) which gives \(2/3\). This is the first fraction which is to be added to the 3, making 3 \(2/3\) which is the approximate root of 13. Since the square of this number is 13 \(4/9\) it is \(4/9\) too large, and if one wishes a closer approximation, the 6 which is the double of the 3 should be added to the fraction \(2/3\), giving 6 \(2/3\) and this number should be divided into the \(4\) which is the difference between 13 and 9, …
- This is the method which is most pleasing to him.
- Don’t despair! He explains what he’s doing in later paragraphs! (Quotes as in (Arcavi & Bruckheimer, 1991))
Approximating radicals
- Let us suppose we are required to find the root of 13. The nearest square is 9, which has root 3. I let the approximate root of 13 be 3 plus 1 tanto unknown.
- Its square is 9 plus 6 tanti p. 1 power. We set this equal to 13.
- Subtracting 9 from either side of the equation we are left with 4 equal to 6 tanti plus one power.
- Many people have neglected the power and merely set 6 tanti, equal to 4. The tanto then comes to \(2/3\).
- and the approximate value of the root is 3 \(2/3\) since it has been set equal to 3 p. 1 tanto.
- However, taking the power into account, if the tanto is equal to \(2/3\), the power will be \(2/3\) of a tanto, which, added to the 6 tanti, will give us 6 and \(2/3\) tanti, which are equal to 4.
- So the tanto will be equal to \(3/5\), and since the appropximate is 3 p. 1 tanto it comes to 3 \(3/5\).
- But if the tanto is equal to 3 \(3/5\), the power will be \(3/5\) of a tanto and we obtain 6 \(3/5\) tanti equal to 4 …
- e cosi procedendo si puo approssimare a una cosa insensible “and this process may be carried to within an imperceptible difference.”
Sketch 29: Beyond the Pale: Irrational Numbers
YBC 7289
Yale Babylonian Collection
:CUSTOMID: ybc-7289
 15
presentation note: use two-finger pinch-out trackpad gesture to zoom on the laptop
15
presentation note: use two-finger pinch-out trackpad gesture to zoom on the laptop
The Fundamental Theorem of Algebra
- Essential statement: Every polynomial of degree \(n\) has \(n\) complex roots.
- Jean d’Alembert (1717-1783)
- Why pursue this theorem?
Finding a counter-example.
- Leibniz (as quoted in (Laubenbacher & Pengelley, 1999, p. 216)): \[x^4 + a^4 = (x^2 + a^2\sqrt{-1})(x^2 - a^2\sqrt{-1})\]
- “Therefore, \(\int dx /(x^4 + a^4)\) cannot be reduced to the squaring of the circle or the hyperbola by our analysis above, but founds a new kind of its own”
Finding a counter-example.
- Nikolaus Bernoulli factors it.
- But this Bernoulli suggests in 1742 (Dunham, 1991a): \[x^4 - 4x^3 + 2x^2 + 4x + 4\] can’t be factored.
- Euler factors it.
- Euler attempts a proof in 1749
- Gauss finally resolves it in 1799.
- Proves that every polynomial with real coefficients can be factored into linear and quadratic factors
- his first of four proofs of the FTA (then 1816, 1816, and 1849)
Finding a Formula - Roots of higher-degree polynomials.
Niels Abel
Brief Bio
- 1802-1829 (Norway)
- Died of tuberculosis.
- Invented group theory
- No general algebraic formula for degree 5 polynomials (1824)
Evariste Galois
- 1811-1832 (France)
- Bad student
- Political revolutionary
- Mathematician
Galois - Mathematician
- Also invented group theory: (Quote in (Laubenbacher & Pengelley, 1999)):
Jump above calculations; group the operations, classify them according to their complexities rather than their appearances; this, I believe, is the mission of future mathematicians; this is the road on which I am embarking in this work
- Field called Galois Theory
- Solutions to polynomial equations (among his final 60 page work)
TODO Day 10
TODO Sketch 14: On Beauty Bare: Euclid’s Plane Geometry
Sketch 13: A Marvelous Proof: Fermat’s Last Theorem
Diophantus
- Diophantus of Alexandria lives around 3rd century AD (probably)
- He quotes Hypsicles (150BC) and is quoted by Theon of Alexandria (350AD)
- A book by the Bishop of Laodicia dedicated a book to Diophantus around 278AD
- What we know is a puzzle:
Diophantus passed 1/6 of his life in childhood, 1/12 in youth, and 1/7 more as a bachelor. Five years after his marriage was born a son who died 4 years before his father, at 1/2 his father’s [final] age
quoted from (Eves, 1990)
What did he do?
- Wrote three works: Arithmetica, On Polygonal Numbers, and Porisms.
- The first we have a lot of (6 of 13 books)
- Second we have fragments
- Third is completely lost.
Arithmetica
- A book on what we now call algebraic number theory
- Deals with 130 problems and solutions
- Problems involved 1st and 2nd degree equations (requiring positive rational solutions)
- No general methods, just solving individually (with clever tricks)
- The Greek contribution to algebra
Diophantus - Example Problems from (Eves, 1990, p. 181)
- Book II, Problem 28
Find two numbers such that their product added to either gives a square number.
- His answer is \(\displaystyle \left(\frac34\right)^2, \left(\frac7{24}\right)^2\).
- Book III, Problem 6
Find three numbers such that their sum is a square and the sum of any pair is a square.
- His answer is \(80, 320, 41\).
After verifying his answers
- … do you think you’d try to find more?
- Are there more answers to a problem? A general formula?
Diophantus - A historical problem
- Book II, problem 8: To divide a given square number into two squares. As quoted in (Katz, 2003, p. 177):
Let it be required to divide 16 into two squares. And let the first square = \(x^2\); then the other will be \(16-x^2\); it shall be required therefore to make \(16-x^2=\) a square. I take a square of the form \((ax-4)^2\), a being any integer and 4 the root of 16; for example, let the side be \(2x-4\), and the square itself \(4x^2 + 16 - 16x\). Then \(4x^2 + 16 - 16x = 16 - x^2\). Add to both sides the negative terms and take like from like. Then \(5x^2 = 16x\), and \(x=16/5\). One number will therefore be 256/25, the other 144/25, and their sum is 400/25 or 16, and each is a square.
Diophantus - A historical problem

Figure 1: Diophantus and Fermat
Diophantus - A historical problem
Solution to Book II, problem 8 suggests general method:
- To find two numbers \(x\) and \(y\) so that \(x^2 + y^2 = b^2\):
- Pick \(a\) to be any number.
- Set \(y=ax-b\)
- Then \(b^2 - x^2 = a^2 x^2 -2abx + b^2\)
- … \(2abx = (a^2+1)x^2\)
- … \(\displaystyle x = \frac{2ab}{a^2+1}\).
- What about other powers?
Hypatia of Alexandria
- Teacher at the University at Alexandria
- Her commentaries:
- Conics of Appollonius
- Edited Almagest of Ptolemy (astronomy / trig) (Almagest is from the Arabic for “Greatest”)
- Edited Theon’s commentary of The Elements
- Arithmetica by Diophantus
- Diophantus: “Father of algebra” and Hypatia: “Mother of algebra”
Diophantus’ Work Lives On
- 1463 - Regiomontanus: Called for a Latin translation of the remaining Greek texts
- 1570 Rafael Bombelli finds the manuscript in the Vatican
- with Antonio Maria Pazzi translates it
- … doesn’t publish it
- uses the problems in his Algebra 1572
- 1575 - Xylander (formerly Wilhelm Holzmann) Translated the Greek and added his commentary
- 1621 - Bachet de Meziriac Published the Greek and Latin together with notes
- 1670 - Clement-Samuel Fermat
“A second, carelessly printed, edition was brought out in 1670” (Eves, 1990, p. 180). This version included his father’s marginal notes.
- Who was his father?
Pierre de Fermat
- Lived 1601-1665
- French lawyer
- Mathematician as a hobby
- Contributions include:
- Calculus
- Probability
- Number Theory
 Marginal notes in Diophantus’ Arithmetica
Marginal notes in Diophantus’ Arithmetica
Proving ALL the things
- Christian Goldbach and Leonhard Euler
- Fermat’s most famous note:
Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.[fn: http://www.textkit.com/greek-latin-forum/viewtopic.php?f=3&t=7108]
Fermat’s Last Theorem(?)
- Conjecture: The expression \(x^n + y^n = z^n\) has no integer solutions for \(n>2\).
Taniyama-Shimura Conjecture
- Conjecture: All elliptic curves are modular.
- Conjectured by Yukata Taniyama and Goro Shimura in 1955.
- (I intended this slide to seem jarring and out of place)
Andrew Wiles (1953-present)
- As a boy (of about 12) read about Fermat’s Conjecture
- … so he gets his PhD in Mathematics
- Becomes and still is a Professor of Mathematics at Oxford
- Worked in a specialized field involving elliptic curves
- Fermat’s Conjecture is a hard problem, don’t work on it
Fermat’s Last Theorem
- 1987: “The Epsilon Conjecture” The Taniyama-Shimura conjecture implies Fermat’s Last Theorem.
- Wiles learns about this result…
- … and spends the next seven years of his professional life proving one of the most difficult results in modern mathematics.
- Proven. 1993.
- … an error.
- Patched up (100ish? pages later) 1994. Completely correct.
- BBC/Horizon’s Documentary on Fermat’s Last Theorem. You can find it on YouTube or Vimeo.
- Accolades for Wiles
TODO Day 11
Sketch 3: Nothing Becomes a number: The Story of Zero
These come from (Kaplan, 2000)
Mayan God of Zero and ritual sacrific (Kaplan, 2000, p. 88)
The Mayan gods of the underworld were governed by the god of death - the God of Zero.
A human would be dressed in the regalia of the God of Zero, and then sacrified by having his lower jaw town off
Roman ways of avoiding zero.
Pliney the Elder.
- 60AD, Pliney is writing an astronomy work and dividing the sky in \(360^\circ\) as has been long done.
- However, he starts his positioning from \(1^\circ\).
- Romans counted Tuesday as three days after Sunday is Tuesday … because Sunday is counted as 1 day.
- Those musical among us use C to E as a “major third” because there are three notes: C, D, E even though there’s only two note increase from C to E.
Fibonacci isn’t sold on zero
Liber Abaci begins with:
(English quote from (Pisano, 1987))
The nine Indian figures are 9 8 7 6 5 4 3 2 1. With these nine figures, and with the sign 0 which the Arabs call zephir any number whatsoever is written.
in writing this, we are getting the Hindu-Arabic numbers brought to the west in 1202, but he’s not including 0 as a first-class number.
Don’t use numerals at all!
- “The old figures alone are used because they cannot be easily falsified. ”(Venetian bookkeeping text)
- University of Paduo books: “non per cifras sed par literas claros” (no numbers, clear letters)
- 1494, Mayor of Frankfurt: “abstain from calculating with digits.”
- 1594, canon in Antwerp: don’t use numerals in contracts
Double-entry bookkeeping
- Basic idea: debits and credits and balance
- Luca Pacioli in 1494 formalized
- Pacioli’s bookkeeping showed readers that 0 is a value not just a sign. It has literal, tangible value like other numbers.
John Napier and ab=0?
- Napier solving ab=0
- This is absolutely obvious to us, and our students do it rote without any thought.
- … but
- Multiplication is repeated addition. 5*7 = 7+7+7+7+7. Fine. a*b = a+a+a+a…+a b times or similarly b+b+b+…+b a times.
- Multiplication is just repeated addition.
- So all that’s really happening in \(ab\) is that we’re adding many things together.
- … but that addition sums to 0.
- This is a balanced ledger.
- This is a conservation of energy law.
- It requires us to hold that 0 is a value and that everything else should be in balance.
- This blew my mind!
The Algorists vs Abacists
Hundreds year long controversy to adopt Hindu-Arabic numerals
- To me, look in notes here
- (we’ll also talk about tally sticks later…)
- Woodcut by Gregor Reisch in Margarita Philosophica It’s called The Allegory of Arithmetic 1503
- Shows Boethius using Hindu Arabic numbers to do calculations while Pythagoras is using a counting board (and looks a bit concerned) (it is thought Pythagoras invented the Greek abacus)
 [fn: Houghton Library / Public domain]
[fn: Houghton Library / Public domain]
- Abacists favored Roman numerals and work with a physical counting device
- Algorists favored the Arabic numerals and algorithms
Accountants against the change:
- The numbers are highly susceptible to fraud (change a digit)
- Too easy to use: (Stone, 1972) #+beginquote [T]he flexibility of the new system would lead to inaccuracies and errors due to the less painstaking efforts on the part of the accountant.
- To me, look here about tally sticks
TODO Day 12
“Nutshell” 26 - 66
The Algorists vs Abacists
Hundreds year long controversy to adopt Hindu-Arabic numerals
- To me, look in notes here
- (we’ll also talk about tally sticks later…)
- Woodcut by Gregor Reisch in Margarita Philosophica It’s called The Allegory of Arithmetic 1503
- Shows Boethius using Hindu Arabic numbers to do calculations while Pythagoras is using a counting board (and looks a bit concerned) (it is thought Pythagoras invented the Greek abacus)
 [fn: Houghton Library / Public domain]
[fn: Houghton Library / Public domain]
- Abacists favored Roman numerals and work with a physical counting device
- Algorists favored the Arabic numerals and algorithms
Accountants against the change:
- The numbers are highly susceptible to fraud (change a digit)
- Too easy to use: (Stone, 1972) #+beginquote [T]he flexibility of the new system would lead to inaccuracies and errors due to the less painstaking efforts on the part of the accountant.
- To me, look here about tally sticks
TODO Sketch 15: In Perfect Shape: The Platonic Solids
Kepler’s mysticism

- inside the orbrit of Saturn is a cube;
- the cube is circumscribed by orbit of Jupiter;
- tetrahedron between Jupiter and Mars,
- dodecahedron between Mars and Earth,
- icosahedron between Earth and Venus,
- octahedron between Venus and Mercury
- he worked out the size of orbits and size of the solids and was very close (except the Platonic solid part)
Dymaxion map / Fuller map
A neat application of an icosahedron.
- invented in 1943 by Buckminster Fuller
- a projection of the globe onto an icosahedron
- can be unfolded in different ways to illustrate different aspects of Earth
- Example images from Wikimedia:
Neat application for human migration
TODO Sketch 16: Shapes by Numbers: Coordinate Geometry
On Plane Loci by Fermat
- Check out On Plane Loci (Smith, 1929)
- Check out the Geogebra activity of Fermat’s geometry.
TODO Day 13
Look at day 14 and later below vvvvv
TODO Day 14
Sketch 18: Half is better: Sine and Cosine
Aryabhata: Arrow fields
In a circle, the product of both arrows, that is the square of the half-chord, certainly for two bow fields.
Aryabhata: Hawk and Rat.
“Just in this case, they relate to hawk and rat examples” (Keller, 2006),
Me: Go to (Keller, 2006, pp. 85–87)
Hipparchus
- circa 180-125bc
- ’Father of Trigonometry’
- Created a table of chords
- … we don’t have them
- Theon tells us there were 12 books
- Used \(\pi = 3;8,30\)
- Used a circle’s circumference divided into 360*60 parts, measured in minutes
- This is (likely) the reason we use 360 parts of a circle
- possibly due to the zodiac
- also Babylonian fractions are better than others
- Egyptian unit fractions were cumbersome
- Greek fractions weren’t convenient otherwise
- … gives diameter of about 6875’
- and radius of about 3438’
- or \(57^\circ 60'\)
Cladius Ptolemy’s Almagest
- Ptolemy (circa 100-170AD)
- Actual Greek name of the book is is Mathematica Syntaxis
- Becomes Almagest in Arabic
Astronomical aside
- Astronomical model:
- the heavens are spherical and rotate as a sphere
- the Earth is a sphere
- the Earth is the center of the cosmos
- the distance from the Earth to the heavens is so big that Earth can be treated as a geometrical point
- the Earth does not move
- Motion kind of makes sense
- Observed retrograde motion of Mars
- Geogebra applet to see it
- Ptolemy’s explanation (draw diagram)
- Geogebra applet to observe his explanation
- … Copernicus explains it later with the Sun at the center.
- Kepler’s model:
- Orbits of the planets lie on ellipses.
- the universe is a bounded sphere
- In his Mysterium cosmographicum (Secret of the Universe) 1596:
- there are six planets
- there are only five Platonic solids
- Coincidence? Obviously not.
- God separated the planets by Platonic solids
- “God is always a geometer.” (Katz, 2003)
(Kozhamthadam, 2002) quoting a letter by Kepler
The sphere possesses a threefold quality: surface, central point, intervening space. The same is true of the motionless universe: the fixed stars, the sun, and the aura or intermediate ether; and it is also true of the Trinity: the Father, the Son, and the Holy Spirit.

- inside the orbrit of Saturn is a cube;
- the cube is circumscribed by orbit of Jupiter;
- tetrahedron between Jupiter and Mars,
- dodecahedron between Mars and Earth,
- icosahedron between Earth and Venus,
- octahedron between Venus and Mercury
- he worked out the size of orbits and size of the solids and was very close (except the Platonic solid part)
Back to Ptolemy’s math
- Suggests his approach is similar to Hipparchus
- Also uses 360 subdivisions of a circle’s circumference
- Further divides into (later Latin translation):
- degree into sixty partes minutae primae
- and these into sixty partes minutae secundae
- Further divides into (later Latin translation):
Ptolemy’s Theorem and sums of chords
For any quadrilateral inscribed in a circle: \[BD\cdot AC = AB \cdot CD + BC \cdot AD\] [[
./images/PtolemyTheorem.png]][By Dicklyon (Wikipedia en Inglés) [Public domain], via Wikimedia Commons]
- The side-lengths of the quadrilateral are chords
- …
- The side-lengths of the quadrilateral are sines of the angles!
 [Kmhkmh (Own work) [CC BY 4.0 (http://creativecommons.org/licenses/by/4.0)], via Wikimedia Commons]
[Kmhkmh (Own work) [CC BY 4.0 (http://creativecommons.org/licenses/by/4.0)], via Wikimedia Commons]
- … you’ll get into Ptolemy’s theorem and the “Star Trek” lemma next month
Ptolemy’s Computation:
- Working in base-60, sexagesimal.
- Letting the diameter of the circle be 120
- This makes the radius 60, which is a unit in sexagesimal
- First, find the chord for \(36^\circ\)
- Side of a regular decagon inscribed in the circle
- Using Euclid II.6 (discussed in class in the algebra notes)
- He finds the chord is \(37;4,55\)
- Second, he found the chord for \(72^\circ\), being \(70; 32, 3\)
- Next, the chord for \(60^\circ\) is \(60\).
- It’s worth remembering: \(\mbox{crd} \alpha = 2R \sin\dfrac\alpha2\)
- … and the values are pretty close
- We also need the Pythagorean Theorem! (To find supplement chords / complementary sines)
- To this point, we have sines for
| Arc \(\alpha\) | \(\alpha/2\) | Chord / Sine \(\alpha/2\) |
|---|---|---|
| \(72^\circ\) | \(36^\circ\) | 70;32,3 |
| \(60^\circ\) | \(30^\circ\) | 60;0,0 |
| \(36^\circ\) | \(18^\circ\) | 37;4,55 |
| \(144^\circ\) | \(72^\circ\) | 114;7,37 |
| \(120^\circ\) | \(60^\circ\) | 103;55,22 |
| \(108^\circ\) | \(54^\circ\) | 97; 4, 55 |
- … he then repeatedly applies his half-angle formula and Pythagorean theorem and halves his way down to under \(1^\circ\).
- (I find this more delightful than you, perhaps…)
- (… but if you want, we can actually do the computations! I have slides for that)
Sketch 27: Counting Ratios: Logarithms
John Napier
- Scottish mathematician
- His father was knighted and was Master of the Mint (his father was 16 when Napier was born)
- Studied Theology
- “violently anti-Catholic” according to (Eves, 1990)
- 1593, A Plaine Discovery of the Whole Revelation of Saint John
- attempts to mathematically prove the Pope was the Antichrist
- end of the world occurs between 1688 and 1700.
- 21 editions of the book were published
- (Eves, 1990) says “Napier sincerely believed that his reputation with posterity would rest upon this book.”
- numerology
- Wizarding stories from (Eves, 1990, p. 308)
- “The black rooster”
- Catching pigeons
- Rabdologia and “lattice multiplication”
- Published Mirifici logarithmorum canonis descripto in 1614
- A description of the wonderful table of logarithms
Seeing there is nothing that is so troublesome to mathematical practice, nor that doth more molest and hinder calculators, than the multiplications, divisions, square and cubical extractions of great numbers … I began therefore to consider in my mind by what certain and ready art I might remove those hindrances.14
Arithmetic Break!
- \(2^3 \cdot 2^2 = \dots\)
- \(10^3 \cdot 10^2 = \dots\)
- \(10^{-7} \cdot 10^{7} = \dots\)
- \(10^7\cdot \left( 1 - 10^{-7}\right) = \dots\)
Arithmetic Break!
Let’s make a table! 14
| n | \(P_n\) | |
|---|---|---|
| 0 | \(10^7\) | |
| 1 | \(10^7\left(1 - 10^{-7} \right)\) | |
| 2 | \(10^7\left(1 - 10^{-7} \right)^2\) | |
| 3 | \(10^7\left(1 - 10^{-7} \right)^3\) | |
| 4 | \(10^7\left(1 - 10^{-7} \right)^4\) |
Arithmetic Break!
Let’s compute a few things:
- \((\sin 90^\circ) \cdot 10,000,000\)
- \((\sin 89^\circ 59') \cdot 10,000,000\)
- \((\sin 89^\circ 58') \cdot 10,000,000\)
- \((\sin 89^\circ 57') \cdot 10,000,000\)
Briggs’ logarithms
base 10 logarithms in 1624 in Arithmetica logarithmica
Slide rule activity
- Let’s explore logarithms and take a look at making a slide rule
Day 15
TODO Sketch 26: Out of the Shadows: The Tangent Function
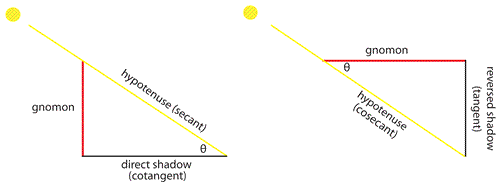
Direct Shadow and Inverse Shadow
Getting by with calculations:
- inverse shadow: \(\displaystyle \frac{\sin \theta}{\sin( 90^\circ - \theta)}\)
- shadow: \(\displaystyle \frac{\sin( 90^\circ - \theta)}{\sin \theta}\)
Gnomon

Bhaskara I on gnomons
- Thoughts on Details Proper Construction
- (Keller, 2006, p. 70) (You’ll notice that he amuses me)
Bhaskara I on computing shadows
- Working proportions of shadows of gnomons
- think about ’shadow of tree’ type from trig class
- (Keller, 2006, p. 74)
- “Say the shadows of the two gnomons which stand respectively at eighty from the foot of a light on a pole whose height is seventy two; and at twenty from <a light whose height is> thirty”
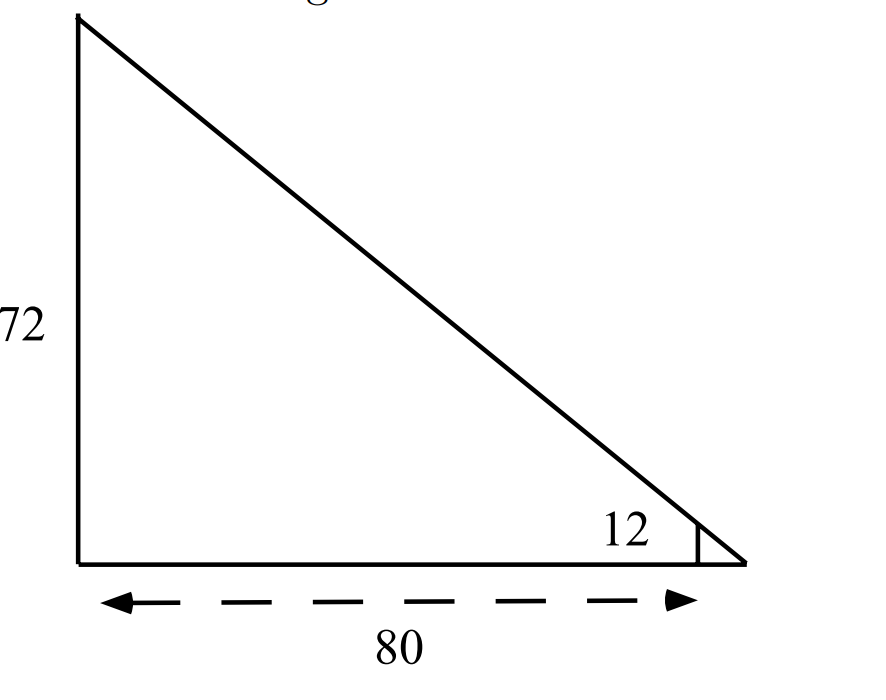
“Setting Down:”
- Distance between the gnomon and base is 80;
- this multiplied by the gnomon is 960.
- The base is 72, the gnomon 12; their difference is 60
- The multiplied 960 is divided by this; “the shadow is obtained: 16.”
Let’s look at all trig functions
- Al-Biruni’s trigonometric lengths
- … Let’s construct all the lines first; then look at the relevant segments
- Imagine sun is in bottom left quadrant https://www.geogebra.org/classic/g8tzvkwa
I’m going to use our notation
Tangent isn’t ’tangent’ or a function, but I’m calling it that; it would be thought of as a shadow
Al-Biruni’s Half angle tangent:

- Formula \(\tan(\theta/2)\)
- \(\displaystyle \tan\left(\frac{\theta}{2}\right) = \frac{\sin\theta}{1 + \cos \theta}\)
Sketch 30: Barely Touching: From Tangents to Derivatives
Early “integration” - area and volume problems
- Hippocrates : Quadrature of the Lune
- Eudoxus (408-355 B.C.)
- Pioneered the Exhaustion Proof
- Archimedes (287-212 B.C.)
- Took the Exhaustion Proof to the next level
- Found the area of a circle (and other curved geometric figures) in organized steps of regular polygons
- How was this done to find the area of the circle?
- Found area of a parabolic sector by a geometric argument of \[\sum_{n=0}^\infty \dfrac{1}{4^n} = \dfrac{4}{3}\]
- Liu Hui (China 3rd century, A.D.) used a similar method of exhaustion re: circles
- Simon Stevin (Flanders, 1548-1620)
- Estimated the pressure on the vertical wall of a water vessel by mentally slicing the wall into thin, horizontal strips
- His work on decimals would later inspire Newton’s Calculus
- just as they were influential for Napier’s logarithms
- Johannes Kepler (1571-1630)
- Volumes of solids of revolution.
- Why?
- Wine barrels!
- Gauging rods were not always an accurate way to measure volume of wine barrels.
- Areas in elliptical orbits (second law of planetary motion)
- Volumes of solids of revolution.
- Bonaventura Cavalieri (1598-1647)
- Rene Descartes (1596-1650)
- Invented “analytic geometry”
- define coordinate axes
- represent a geometric curve on the axes in terms of variable expression
- Method for finding tangent line to some curves; ’higher parabolas’ \(x^n\)
- intersecting a circle with the curve
- Invented “analytic geometry”
- Pierre de Fermat (1601-1665)
- Invented “analytic geometry” (also)
- found area under some geometric curves; ’higher parabolas’ \(x^n\)
- found connection between area and tangent questions for some curves
- that’s the fundamental theorem, but didn’t quite connect the dots!
Early Differentiation
- Fermat is foundational in this:
- Found maximum and minimum values of curves
- places where the slope of the tangent line is 0
- we call this “Fermat’s theorem” in calculus
- Example: (using Viete’s notation of vowels are variables):
- Divide a quantity into two parts such their product is a maximum
- Let \(B\) be a given quantity; denote points on a curve by by \(A\) and \(B-A\). Assume \(E\) is a really small variable (like \(\epsilon\)):
- \[(A-E)[B-(A-E)] = A(B-A)\]
- because \(E\) is really, really small. Basically but not zero..
- Algebra…
- \[2AE - BE - E^2 =0\]
- \[2AE - BE - E^2 =0\]
- Divide through by E (which isn’t zero, remember?)
- \[2A - B - E = 0\]
- Now set \(E = 0\); (it wasn’t zero before! Promise!)
- \[2A = B\]
- The maximum of the curve occurs when \(A = B/2\).
- This is \(\displaystyle \lim_{\epsilon \to 0} \frac{f(x+\epsilon) - f(x)}{\epsilon} = 0\)
- Fermat’s Method of finding tangents to curves given a Cartesian equation by finding subtangents
- the horizontal distance on the \(x\) axis from the \(x\) point to where the tangent would intersect. On the picture below, this tracing the value \(a\) to the left.
- assume we’re at point \((x,y)\) and want to find the subtangent \(a\); \(e\) is a small infinitessimal quantity
- Use The fact that we have similar triangles (whose hypotenuses) are the tangent: \[ \frac{a}{y} = \frac{e}{\text{vertical}}\]
- The Cartesian coordinates are given here; and now pretend it’s on the curve
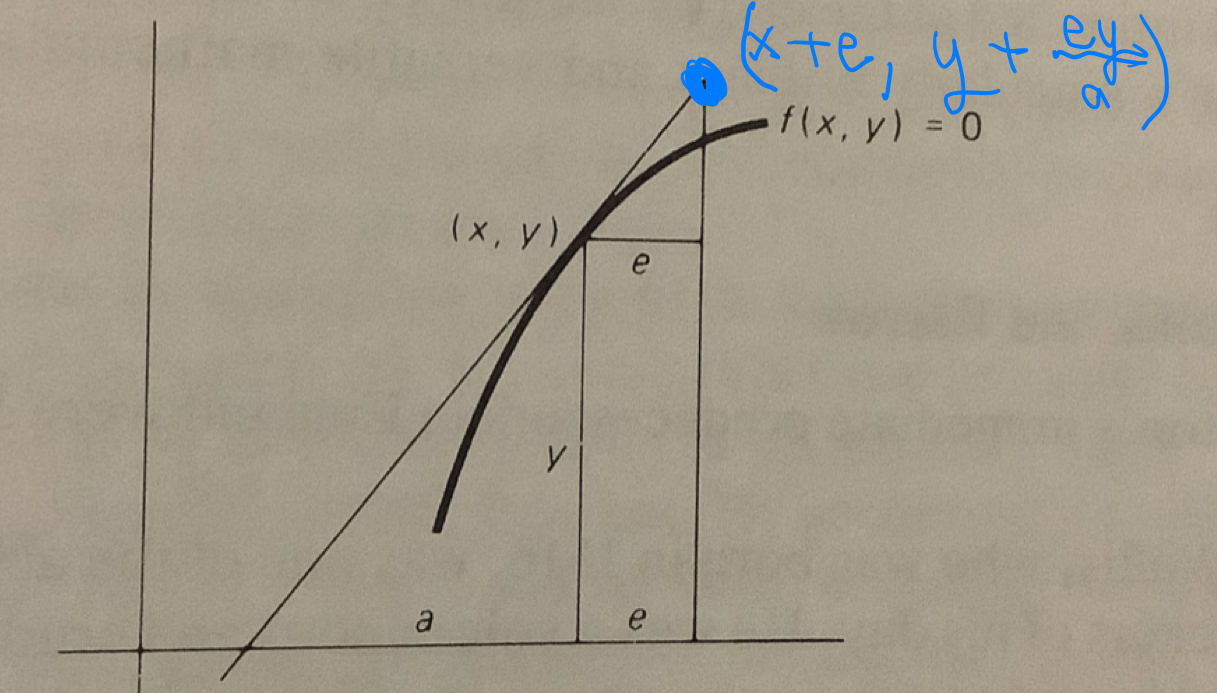
- Set \(f(x + e, y + \frac{ey}{a}) = 0\)
- Algebra… divide everything by \(e\) (it’s not zero!)
- Then pretend that \(e\) was zero the whole time and solve for \(a\).
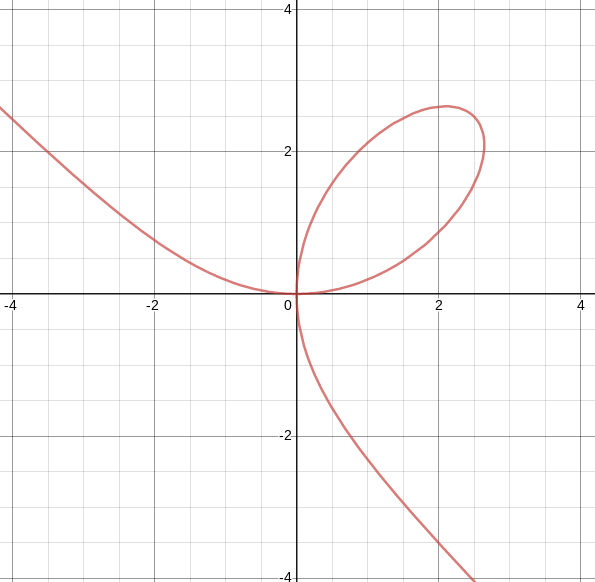
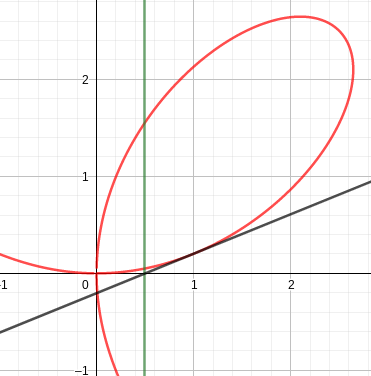
- Specific Fermat example is for the ’folium of Descartes’ (letter to Mersenne in June 1638) \[x^3 + y^3 = nxy\] (this picture has \(n=5\))
- Set \(f(x + e, y + \frac{ey}{a}) = 0\)
- \((x+e)^3 + y^3(1+\frac{e}{a})^3 - ny(x+e)(1+\frac{e}{a}) = 0\)
- … tedious algebra…
- \(e\left( 3x^2 + \frac{3y^3}{a} - \frac{nxy}{a} - ny\right) + e^2 \left( 3x + \frac{3y^3}{a} - \frac{ny}{a} \right) + e^3 \left( 1 + \frac{y^3}{a^3}\right) = 0\)
- divide everything by \(e\)
- … set \(e = 0\) and solve for \(a\)
- \(\displaystyle a = -\frac{3y^3 - nxy}{3x^2-ny}\)
- If \((x, y) = (1, 0.20164)\) and \(n=5\), we find the subtangent to be \(a= 0.493827\). Plotting the actual tangent to the curve, we find:
Isaac Barrow
Newton’s fluxional calculus
Before we get to Newton… Edmond Halley in 1684 discussed Kepler’s third law of motion:
The square of a planet’s orbital period is proportional to the cube of the length of the semi-major axis of its orbit.
- Halley suggested this implied the attraction of the sun was the inverse of the square of the distance to the planetary bodies.
- Christopher Wren challenged Halley and Robert Hooke to show that the inverse square law implied the planet had an elliptic orbit (with a 40 shilling wager). (Cook, 1991)
- Neither Halley and Hooke did it.
- Halley poses the question to Newton.
- Newton thinks a bit.
- Within two years he “invents” physics and calculus.
- He should publish a book!
- Now, let’s talk about Fishes
- Royal Society and Historia Piscium, published 1686
- Expensive for very detailed engravings
- Halley and Hooke being paid £50 for their work
- 🐟How about 50 fish books!?!?🐠
Now let’s talk about Newton’s fluxional calculus
- A fluent is a point or a line in motion
- A fluxion is the velocity of that motion
The method “shortly explained rather than accurately demonstrated.” (Newton quoted in (Boyer, 1988))
We’ll work an example!
- “Arrange according to the dimensions of some fluent quantity, say x, and”
- Multiply its terms by any arithmetical progression [ending in 0]
- then by \(\dfrac{\dot{x}{x}}\)
- Carroy out this operation separately for each one of the fluent quantities, then put the sum of the products equal to nothing, and you have the desired equation.
We’ll “accurately demonstrate” it!
- Binomial theorem!
TODO Day 16
Sketch 21: What’s in a Game? The Start of Probability Theory
- Discuss the Problem of Points and work it out according to Pascal and Fermat.
Notes on Pacal/Fermat
- Keith Devlin (Devlin, 2010) The Pascal-Fermat Correspondence: how mathematics is really done
- Quote from the article “some of them [mathematicians] even went so far as to declare the that the problem could not be solved. Now where have you heard that before?”
English translation of their correspondence: https://www.york.ac.uk/depts/maths/histstat/pascal.pdf
Letters also appear in (Smith, 1929)
- Buffon Needle problem simulator
- https://mste.illinois.edu/activity/buffon/
- there’s also a 1974 article linked here https://www-jstor-org.proxy.wichita.edu/stable/27959621
Sketch 22: Making Sense of Data: Statistics become a science
Discussing (Salsburg, 2002)
- Lady Tasting Tea
- Tea party at Cambridge in the 1920s
- A lady says she can tell whether milk is added before or after
- Ronald Fisher comes up with scheme to test this!
- Can’t use one cup. Why?
- Can’t use two cups, why?
- could guess one and opposite
- entirely correct or entirely wrong
- Or what if she made a mistake one time?
- Need more cups
- Briefly about Ronald Fisher
- Works at Rothamsted Agricultural Experimental Station
- They had gathered 90 years of fertilizer data
- Rothamsted uses formulas to “adjust” data to compare year to year
- calls these ’fertility indexes’
- Fisher looks at it
- Fisher looks at rival companies
- Fisher notices it’s the same non-sense
- Publishes in 1921 that there is no difference what index is used
- in fact, weather was a better predictor than fertilizer
- 90 years of data collection was worthless
- Experimental Design
- Fisher writes The Design of Experiments in 1935
- Chapter 2 is about the lady tasting tea
- Come up with a mathematical model for what you’re measuring
- then collect data
- Includes several exmaples including agriculture, but the book is hard
- It grows in popularity
- Lady tasting tea?
- Fisher describes the story but doesn’t say it’s true
- someone who is there says it is
- … and they say she got every cup right.
- Sir Francis Galton and measurement
- Half cousin of Charles Darwin
- Galton discovered uniqueness of fingerprints
- Wanted to study inheritance of intelligence
- … no good meaure in the 1890s
- Founds a biometrical laboratory to measure parts that are measurable
- Discovers regression to the mean (specifically tall and short)
- realized can’t not revert to the mean
- if tall people always had tall children on average…
- discovered mathematical relationship for reversion to the mean
- called it the coefficient of correlation
- Pearson and Distributions
- Karl Pearson (English mathematician)
- founded first statistics department in the world (1911)
- If you conduct experiment, get scatter of numbers
- … e.g. measuring speed of light or gravity
- or heights or arm length, or ….
- Karl Peason says these things form a mathematical distribution
- there are our numbers that completely describe it
- called parameters from Greek for ’almost measure’
- mean: central value around which measurements scatter
- standard deviation: how far most scatter about the mean
- symmetry: degree to which measurements cluster on one side of the mean
- kurtosis: how far rare measurements scatter from the mean
- Pearson believes that there are true values for anything being measured
- e.g. there is a human male height which is the true mean of all possible measures
- he’s not right (Fisher shows this later)
- Galton founds Biometrika
- Galton wants to study more and more
- Pearson takes over in 1897 and sends women compute the four numbers
- these women are called calculators
- Galton and Pearson found the journal Biometrika
- Galton invests a significant amount of money
- it’s the first journal with color print
- Goal is to prove Darwin’s theory of evolution
- Show a change in the four parameters of species
- Didn’t quite do it, but…
- Did show via measurements of cranial capacity of ancient skulls vs. modern, little change
- Did disprove claims by Australians that aborigines aren’t human (they are)
- … didn’t show survival of the fittest
- Scientists accept it now as correct
- No longer looking for four parameters to try to prove it
- Pearson’s ideas, though, live on:
- economics, sociology, psychology, quantum physics, etc
- we use these distributions and parameters to study a lot
Day 17
Agenda for the day
- MTA Projects
- Reading discussions
- Non-Euclidean geometry
The World is Round.
Okay, some people thought it was flat
- Mesopotamian tablet BM 92687 (about 6th century BC)
- The oldest world map is flat Imago Mundi

There were other ancient flat-Earthers
- Greece - Homer
- Ancient Norse/Germanic people.
- Yggdrasil, the world tree, is actually the center of the disk
But the Earth is round.
Eratostothenes (276-194 BC)
- Learns about the sun at noon in Syrene, Egypt lighting up a well so the sun is straight up
- The next year, same day, in Alexandria at noon the sun cast a shadow of a vertical pole
- Ideas why this suggests the Earth is round?
- Here’s a picture:
- How can we compute the circumference of the Earth?
- (using kilometers, rather than stadia, which he used)
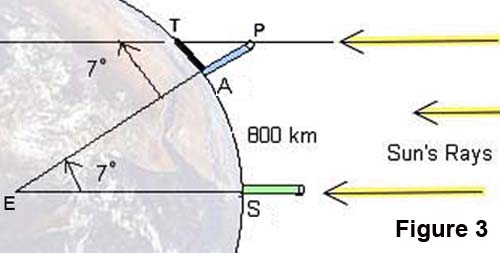
- He’s pretty close
Later, 1037AD, al-Biruni applied trig (from India?) to find the circumference within 1% of the correct value!
- using the astrolabe (thanks Hypatia) helps
Why did Columbus think he found Asia?
- using maps that were too small
- measured circumference 25% too small
- oops
Sketch 19: Strange New Worlds: The Non-Euclidean Geometry
Euclid’s Elements
- The version we know and love
- Playfair’s axiom
There is at most one line parallel to a given line passing through a given point.
- But this isn’t the original version
- The five postulates
- A straight line segment can be drawn joining any two points.
- Any straight line segment can be extended indefinitely in a straight line.
- Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.
- All right angles are congruent.
- If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough.
- The fifth postulate
- Sure is really long…
- Euclid didn’t even use the postulate until proving proposition I.29.
- Maybe it’s not an axiom?
- Attempts to prove it
- Ptolemy attempted a proof
- Proclus tells us about it. That it’s wrong.
- Then Proclus writes an incorrect proof.
- Note to self: A description is in my note archive.
- Omar Khayyam attempts a proof
- …
- Later Lambert attempted a proof
- Ptolemy attempted a proof
Brief Bio of Carl Friedrich Gauss
- 1777 - 1855 in Germany
- School story (6 or 10 years old)
- at 14, Duke of Brunswick gives financial support to him
- Proves regular polygon of 17 sides can be constructed
- 1801, published Disquisitiones Arithmeticae foundation of modern number theory
- Proof of the fundamental theorem of algebra (age 22)
- Age 24, method of least squares and Ceres
- Married Johanna Ostaf in 1805
- Legitimately in love. (quote in logseq notes)
- Becomes director of Gottingen observatory in 1807
- 1808, wife dies giving birth to second kid
- Legitimately devastated. (quote in archive notes)
- marries Minna, best friend of first wife.
- 1809, work on celestial bodies
- Work in analysis in 1816
- 1818 geodesic (curved map) survey of Hanover;
- (non-Euclidean geometry; we’ll come back to this)
- 1830s physics, for example gravitation, magnetism
- as a hobby-ish, built a telegraph that could send over 5,000 feet
- differential geometry
- … lots of other things
- many famous students, including Riemann
- Minna’s death story
Curvature
- Two-dimensional curvature
- Lines have zero curvature
- Circles have constant curvature
- Other “curves” (e.g. parabolas) have variable curvature
- “hill” is positive curvature
- “valley” is negative curvature
- Three-dimensional curvature
- Planes have zero curvature (e.g. the floor)
- Positive curvature
 [Evan-Amos [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)]]
[Evan-Amos [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)]]
- Negative curvature
 [Evan-Amos [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)]]
[Evan-Amos [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)]]
- To the high-quality document camera!!!
- https://obs.ninja/?view=UUyG9aU

- Physical models (crochet!)
- Constant positive curvature example
- this elliptic geometry
- Constant negative curvature
- this hyperbolic geometry
- Constant positive curvature example
- Does an ant walking on a ball know it’s walking on a ball?
- In calc 3, we find the curvature of a sphere is \(\dfrac{1}{R^2}\) with \(R\) the radius
- the bigger the sphere, the less curved the sphere
- We see a ball is round because we’re outside the ball, looking on
- If you’re standing on a surface, can you, without leaving it, determine its curvature?
- positive, negative, zero?
- Measuring “intrinsic curvature”
- Here, “intrinsic” means a property that can be seen within the object itself
- not from a higher dimension
Gauss, as a surveyor; two approaches
- Circles:
- put a stake in the ground
- tie a long rope around it.
- measure out the circumference of a circle centered at your stake.
- divide the circumference by two times the length of the rope (i.e. diameter)
- if ratio \(= \pi\), it’s flat: zero curvature
- if ratio \(\lt \pi\), positive curvature
- if ratio \(\gt \pi\), negative curvature
- Triangles:
- put three stakes on the ground, somewhat far apart
- tie ropes to each stake
- measure the angles between each rope.
- If the sum of the angles \(=180^\circ\), it’s flat; zero curvature
- If the sum of the angles \(\lt 180^\circ\), it’s negative curvature
- If the sum of the angles \(\gt 180^\circ\), it’s positive curvature
- Circles:
- Here, “intrinsic” means a property that can be seen within the object itself
Logically consistent geometries
- Janos Bolyai (1802-1860)
- His dad, Farkas Bolyai was a mathematician and friend of Gauss
- at age 12, Janos read first six books of Euclid’s Elements
- accomplished violinist
- Studied at the Royal Engineering Academy
- became an Engineer in the Austrian army
- retired after 10 years in 1833.
- … while training with the army… Parallel…Postulate….
- Father’s warning
- Ignores dad.
- 1823:
All I can say now is that I have created a new and different world out of nothing.
 [lacihobo [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)]]
[lacihobo [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)]]
- Farkas, his dad, is excited. Publish immediately!
- Farkas sends a copy to Gauss
- Gauss’ reply
- Nokolai Lobachevsky (1792 - 1856)
- Studied at Kazan University under a former teacher and friend of Carl Gauss
- Degrees in physics and mathematics, became math professor
- in 1829, and in Russian
- replaces the parallel postulate with “more than one line”
- (independent of Gauss and Bolyai)
- Shows sum of angles in a triangle is always less than two right angles
- … and gets smaller the larger the triangle
Sketch 25: Beyond Counting: Infinity and the Theory of Sets
Classic View of Infinity
- Zeno and paradoxes
- Example: Achilles and hare
- Can’t accumulate to infinity; meaningless
- Aristotle says nah;
Actual infinite is bad
\(\infty\) isn’t a number
Potential infinite is good
Largest number ever? Add one.
- Euclid was with Aristotle
- “Infinitely many primes” is actually “Prime numbers are more than any assigned magnitude of prime numbers”
- Basically everyone had this view for 2000 years
- (probably people here, too)
How do we tell that two sets are the same size?
- Fingers on hand
- chairs to humans
- etc
- bijections: one-to-one correspondence
Galileo’s Paradox
- Line up every counting number with a square.
- Square numbers are ’sparse’
- So that line up is meaningless!
- PARADOX!!!
- I mean, I disagree
- Can’t talk about \(<, >, =\) of infinite sets
Countable Sets
- A set is said to be countable if there exists a one-to-one correspondence with the natural numbers.
- Examples
- The set of even numbers, {2, 4, 6, 8, …}, is countable since we have the one-to-one correspondence n <-> 2n.
- Galilleo’s paradox: The set of square numbers, is countable since we have the one-to-one correspondence \(n\) <-> \(n^2\)
- The set of powers of 2, {2, 4, 8, 16, …}, is countable, with the one-to-one correspondence n <-> \(2^n\)
- …
Georg Cantor
- Born March 3, 1845 in St. Petersburg, Russia, died January 6, 1918 in Halle, Germany.
- Family moved to Germany when he was 12
- Completed his doctorate at the University of Berlin in 1867 under Weierstrass
- In 1874 he published a paper which fundamentally changed the way we think of infinity.
- Even Gauss had said, “I protest above all against the use of an infinite quantity as a completed one, which is mathematics is never allowed. The Infinite is only a manner of speaking” [quoted from ref:Dunham1991]

The integers are countable
- We can place the set of all integers (positive, negative, and zero) in one-to-one correspondence via the mapping: \[n \leftrightarrow \frac{1+(-1)^n(2n-1)}{4}\]
- (check examples)
- So they have the same cardinality (size of a set). He called this \(\aleph_0\)
The rational numbers are countable
- Draw the number array!
Reductio ad Absurdum
- A logical statement can only be true or false (it can’t be both).
- We assume the opposite of a statement (logical negation), and then through argumentation derive a logical contraction:
- Ex: “Assume that the square root of two is rational…. We proved that it is not rational.”
- It can’t be both rational and non-rational, and since our assumption (IS rational) was wrong, it must be that (NOT IS RATIONAL or irrational)
Cantor’s Diagonalization Theorem
- The interval of real numbers between 0 and 1 is not denumerable. (Cantor in his 1874 paper)
- Proof by contradiction – the reductio ad absurdum:
- Our assumption: Let’s assume that the interval IS denumerable and find this gives a contradiction.
- If the interval (0, 1) IS countable, what does that mean? There is a one-to-one correspondence with the set of natural numbers.
- Every number between 0 and 1 is on the right side of the table. …. I’ll draw the table in a moment
- To arrive at the contradiction, we will construct number that is not on the list.
- Do the proof… Blow some minds.
\(\infty \ge \infty\)?
- But the set of ALL real numbers is an infinite collection of all of these infinite, uncountable intervals. So surely it’s bigger…
- …Right?
- No.
- The cardinality of all real numbers is the same as the cardinality of the interval (0, 1):
- Consider the one-to-one correspondence:
- \(f(x) = \dfrac{2x-1}{x-x^2}\) from \((0,1) \to \mathbb{R}\).
Which is bigger? \(\mathbb{Q}\) or Irrationals?
- To answer the question formally, we need only one more theorem:
- Theorem: If B and C are denumerable (countable) sets and A is the set of all elements belonging to B or C or both, then A is also denumerable.
- (We can prove it, but we’ll go without proof… unless you want one)
- We know that if B and C are countable, then the union A = B U C is countable.
- So if the set of rationals and irrationals were the same size (countably infinite), then their union would be countable:
- {Real numbers} = {rationals} union {irrationals}
- But the set of real numbers is NOT countable.
- So the set of irrational numbers is also not countable!
Algebraic vs. Transcendental
- An algebraic number is one which is a solution to some polynomial with rational coefficients.
- A transcendental number is one that is not algebraic. We know \(\pi\), \(e\), and some others.
- Cantor didn’t.
- Lindemann wouldn’t prove \(\pi\) was transcendental for a decade!
- Cantor showed that the set of algebraic numbers is countable (a little beyond this class. If we had another class or two on the topic…)
- So all though the algebraic numbers (which include any conceivable roots of numbers) are nearly every number we can possibly imagine. And we can only imagine a handful of transcendentals
- There are vastly more transcendental numbers in the numeric universe!
Cantor does vastly more than this
- 1877 shows \(|(0,1) \times (0,1)| = |(0,1)|\)
- “I see it, but I don’t believe it.”
Is told to quit by respected colleague Mittag-Leffler: (Laubenbacher & Pengelley, 1999)
I am convinced that the publication of your new work… will greatly damage your reputation among mathematicians… but in this way, you will exercise no significant influence, which you naturally desire as does everyone who carries out scientific research.
- Quits mathematics
- Back to theology!
- Theologians love his work on infinite sets!
- 1895 publishes Beiträge zur Begründung der transfiniten Mengenlehre
- Discussing cardinalities of sets, showed that:
- \(|\mathcal{P}(A)| > |A|\) for any set \(A\). (Called “Cantor’s Theorem”)
- “In place of a given set L, another set M can be placed which is of greater power than L”
- … our term ’power sets’
- \(\aleph_0 < |(0,1)| < |\mathcal{P}((0,1))| < |\mathcal{P}(\mathcal{P}((0,1)))| < \dots\)
- an infinite chain of transfinite numbers
- … changed math forever
TODO Day 17
Sketch 23: Machines that Think? Electronic Computers
Idyllic world
Aristotle Quote in (Ifrah, 2001, p. 105)
Suppose every instrument could by command or by anticipation of the need execute its function on its own; suppose that spindles could weave of their own accord, and plectra strike the strings of zithers by themselves; then craftsmen would have no need of hand-work, and masters have no need of slaves.
Computing Devices
- Abacus
- Napier’s Bones (interactive html5)
- These don’t mechanize computing
- They help us count
- We still have to do manual work
Why did it take so long?
- Greeks had mechanics (Archimedes, for example)
- Heron built steam-powered machines
- One theory from (Ifrah, 2001):
- lack of a positional number system with zero
- lack of a need to do tons of computations
- Science progressed (exploded) in the 16th and 17th centuries
- see also Newton, the Bernoullis, Lagrange, Laplace, …
- doing science was tied to mathematical computation
Early computing machines
- 1525 - a pedometer
Invented by Jean Errard de Bel-le-Duc (Ifrah, 2001, p. 124):
A new geographical instrument which, attached to a horse’s saddle, uses the horse’s steps to display the length of the journey one has made … by which one can exactly measure the circuit of a place or the length of a journey“
- He made the old-timey FitBit!
First automatic calculator: the “calculating clock” 1623 by German astronomer Wilhelm Schickard (1592-1635)
- Here’s a working model built from Schickhard’s notes in 1960

- Strickard described it to Kepler in 1623 (letter dated September 20, 1623)
- Only copy of the machine was burned in a fire on February 22, 1624.
- Pascaline 1642 - how it works (linked on “Additional Resources”): Recommend to watch it on at least 1.5 speed because he talks really slowly https://www.youtube.com/watch?v=3h71HAJWnVU
- Leibniz stepped-reckoner 1694
- lots of time passes, lots of machines
- Thomas de Colmar’s Arithmometer in 1822
- reliable, functional, successful commercially
- marketed in many countries with different names:
- “Saxonia, Archimedes, Unitas, TIM”
- guess what the last one means
- “Time is Money”
- … side track
- Keyboards were invented in the mid-1800’s
- but were fiddly; error prone
- (side note: why QWERTY?)
- First printer invented in 1872
- First calculator with a keyboard and printer in 1882
- Marketed as a cash register
- help solve disputes with customers
Of course, Babbage
- Babbage’s difference engine with relaxing music https://www.youtube.com/watch?v=be1EM3gQkAY
- This video demos the math behind the machine https://www.youtube.com/watch?v=PFMBU17eo_4
For more information
History of Computing in ComputerWorld 1981 https://archive.org/details/TheHistoryOfComputing/mode/2up
- Pascaline - how it works:
https://www.youtube.com/watch?v=3h71HAJWnVU Recommend to watch it on at least 1.5 speed because he talks really slowly
- Babbage’s difference engine with relaxing music
https://www.youtube.com/watch?v=be1EM3gQkAY
- This video demos the math behind the machine https://www.youtube.com/watch?v=PFMBU17eo_4
- ENIAC
Really great photo collection from the Computer museum
- setting it up https://www.computerhistory.org/revolution/birth-of-the-computer/4/78/316
- operating it https://www.computerhistory.org/revolution/birth-of-the-computer/4/78/321
- implemented in a circuit chip in 1995: https://www.computerhistory.org/revolution/birth-of-the-computer/4/78/327
Sketch 24: The Arithmetic of Reasoning: Boolean Algebra
Binary thinking
- Leibniz invents binary number system - using 0’s and 1’s published in 1703 Explication de l’Arithmétique Binaire
- Has addition, subtraction, multiplication, and division
- Acknowledges the earlier work of Fuxi and the “mystery of lines” (Note: Fuxi is said to be the inventor of Chinese writing)
Leibniz’ binary system was philosophical - Laplace wrote, as in (Ifrah, 2001, p. 89):
In the binary system which he invented, Leibniz sought to perceive the Creation. He imagined that the Unity stood for God and Zero for the Void, that the Supreme Being had drawn every existing thing out of the void just as unity and zero suffice to represent every possible number in the system…
… I mention this merely to show how childish fancies can cloud the visions of even the most distinguished men.
Old-timey burn!
Yijing the Book of Changes
- Yijing and yin and yang
- yin is “female” and represented by a broken line: - -
- yang is “male” and represented by a contiuous line: —
- Use trigrams (three lines) or hexagrams (six lines)
Summer, the South, the sky, the Sun (solid lines…)
--- --- ---
Winter, the North, the Earth, the Moon:
- - - - - -
- (boolean negations)
Thunder, the Northeast, coming of Spring:
- - --- - -
Wind, the Southwest, end of Summer:
--- - - ---
- trigrams represent \(2^3 = 8\) possibilties
- hexagrams represent \(2^6 = 64\) possibilities
- the ability to negate terms, as well as combine them
- we’d call them join and meet
- … or call them and and or
- Later this is a Boolean Algebra we study in Math 322
- equivalent to \(\cup, \cap\) in set theory in 501.
George Boole
Laws of Thought https://www.gutenberg.org/files/15114/15114-pdf.pdf
De Morgan:
Formal Logic by de Morgan https://archive.org/details/formallogicorthe00demouoft
Trig and double algebra https://archive.org/details/ost-math-trigonometry_and_double_algebra/page/n7/mode/2up
Memoirs (by his wife) https://archive.org/details/memoirofaugustus00demouoft/page/n11/mode/2up
A Budget of Paradoxes https://archive.org/details/budgetofparadoxe00demouoft/page/22/mode/2up
TODO Day 18
The World is Round.
Okay, some people thought it was flat
- Mesopotamian tablet BM 92687 (about 6th century BC)
- The oldest world map is flat Imago Mundi

There were other ancient flat-Earthers
- Greece - Homer
- Ancient Norse/Germanic people.
- Yggdrasil, the world tree, is actually the center of the disk
But the Earth is round.
Eratostothenes (276-194 BC)
- Learns about the sun at noon in Syrene, Egypt lighting up a well so the sun is straight up
- The next year, same day, in Alexandria at noon the sun cast a shadow of a vertical pole

- Ideas why this suggests the Earth is round?
- Here’s a picture:

- How can we compute the circumference of the Earth?
- (using kilometers, rather than stadia, which he used)

- He’s pretty close
Later, 1037AD, al-Biruni applied trig (from India?) to find the circumference within 1% of the correct value!
- using the astrolabe (thanks Hypatia) helps
Why did Columbus think he found Asia?
- using maps that were too small
- measured circumference 25% too small
- oops
Sketch 19: Strange New Worlds: The Non-Euclidean Geometry
Euclid’s Elements
- The version we know and love
- Playfair’s axiom
There is at most one line parallel to a given line passing through a given point.
- But this isn’t the original version
- The five postulates
- A straight line segment can be drawn joining any two points.
- Any straight line segment can be extended indefinitely in a straight line.
- Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.
- All right angles are congruent.
- If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough.
- The fifth postulate
- Sure is really long…
- Euclid didn’t even use the postulate until proving proposition I.29.
- Maybe it’s not an axiom?
- Attempts to prove it
- Ptolemy attempted a proof
- Proclus tells us about it. That it’s wrong.
- Then Proclus writes an incorrect proof.
- Note to self: A description is in my note archive.
- Omar Khayyam attempts a proof
- …
- Later Lambert attempted a proof
- Ptolemy attempted a proof
Brief Bio of Carl Friedrich Gauss
- 1777 - 1855 in Germany
- School story (6 or 10 years old)
- at 14, Duke of Brunswick gives financial support to him
- Proves regular polygon of 17 sides can be constructed
- 1801, published Disquisitiones Arithmeticae foundation of modern number theory
- Proof of the fundamental theorem of algebra (age 22)
- Age 24, method of least squares and Ceres
- Married Johanna Ostaf in 1805
- Legitimately in love. (quote in logseq notes)
- Becomes director of Gottingen observatory in 1807
- 1808, wife dies giving birth to second kid
- Legitimately devastated. (quote in archive notes)
- marries Minna, best friend of first wife.
- 1809, work on celestial bodies
- Work in analysis in 1816
- 1818 geodesic (curved map) survey of Hanover;
- (non-Euclidean geometry; we’ll come back to this)
- 1830s physics, for example gravitation, magnetism
- as a hobby-ish, built a telegraph that could send over 5,000 feet
- differential geometry
- … lots of other things
- many famous students, including Riemann
- Minna’s death story
Curvature
- Two-dimensional curvature
- Lines have zero curvature
- Circles have constant curvature
- Other “curves” (e.g. parabolas) have variable curvature
- “hill” is positive curvature
- “valley” is negative curvature
- Three-dimensional curvature
- Planes have zero curvature (e.g. the floor)
- Positive curvature
 [Evan-Amos [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)]]
[Evan-Amos [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)]]
- Negative curvature
 [Evan-Amos [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)]]
[Evan-Amos [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)]]
- Physical models (crochet!)
- Constant positive curvature example
- this elliptic geometry
- Constant negative curvature
- this hyperbolic geometry
- Constant positive curvature example
- Does an ant walking on a ball know it’s walking on a ball?
- In calc 3, we find the curvature of a sphere is \(\dfrac{1}{R^2}\) with \(R\) the radius
- the bigger the sphere, the less curved the sphere
- We see a ball is round because we’re outside the ball, looking on
- If you’re standing on a surface, can you, without leaving it, determine its curvature?
- positive, negative, zero?
- Measuring “intrinsic curvature”
- Here, “intrinsic” means a property that can be seen within the object itself
- not from a higher dimension
Gauss, as a surveyor; two approaches
- Circles:
- put a stake in the ground
- tie a long rope around it.
- measure out the circumference of a circle centered at your stake.
- divide the circumference by two times the length of the rope (i.e. diameter)
- if ratio \(= \pi\), it’s flat: zero curvature
- if ratio \(\lt \pi\), positive curvature
- if ratio \(\gt \pi\), negative curvature
- Triangles:
- put three stakes on the ground, somewhat far apart
- tie ropes to each stake
- measure the angles between each rope.
- If the sum of the angles \(=180^\circ\), it’s flat; zero curvature
- If the sum of the angles \(\lt 180^\circ\), it’s negative curvature
- If the sum of the angles \(\gt 180^\circ\), it’s positive curvature
- Circles:
- Here, “intrinsic” means a property that can be seen within the object itself
Logically consistent geometries
- Janos Bolyai (1802-1860)
- His dad, Farkas Bolyai was a mathematician and friend of Gauss
- at age 12, Janos read first six books of Euclid’s Elements
- accomplished violinist
- Studied at the Royal Engineering Academy
- became an Engineer in the Austrian army
- retired after 10 years in 1833.
- … while training with the army… Parallel…Postulate….
- Father’s warning
- Ignores dad.
- 1823:
All I can say now is that I have created a new and different world out of nothing.
 [lacihobo [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)]]
[lacihobo [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)]]
- Farkas, his dad, is excited. Publish immediately!
- Farkas sends a copy to Gauss
- Gauss’ reply
- Nokolai Lobachevsky (1792 - 1856)
- Studied at Kazan University under a former teacher and friend of Carl Gauss
- Degrees in physics and mathematics, became math professor
- in 1829, and in Russian
- replaces the parallel postulate with “more than one line”
- (independent of Gauss and Bolyai)
- Shows sum of angles in a triangle is always less than two right angles
- … and gets smaller the larger the triangle
Sketch 20: In the eye of the beholder: projective geometry
TODO Day 19
TODO Sketch 6: By tens and tenths: Metric Measurement
TODO Sketch 25: Beyond Counting: Infinity and the Theory of Sets
Classic View of Infinity
- Zeno and paradoxes
- Example: Achilles and hare
- Can’t accumulate to infinity; meaningless
- Aristotle says nah;
Actual infinite is bad
\(\infty\) isn’t a number
Potential infinite is good
Largest number ever? Add one.
- Euclid was with Aristotle
- “Infinitely many primes” is actually “Prime numbers are more than any assigned magnitude of prime numbers”
- Basically everyone had this view for 2000 years
- (probably people here, too)
How do we tell that two sets are the same size?
- Fingers on hand
- People in chairs
- etc
- bijections: one-to-one correspondence
Galileo’s Paradox
- Line up every counting number with a square.
- Square numbers are ’sparse’
- So that line up is meaningless!
- PARADOX!!!
- I mean, I disgree
- Can’t talk about \(<, >, =\) of infinite sets
Countable Sets
- A set is said to be countable if there exists a one-to-one correspondence with the natural numbers.
- Examples
- The set of even numbers, {2, 4, 6, 8, …}, is countable since we have the one-to-one correspondence n <-> 2n.
- Galilleo’s paradox: The set of square numbers, is countable since we have the one-to-one correspondence \(n\) <-> \(n^2\)
- The set of powers of 2, {2, 4, 8, 16, …}, is countable, with the one-to-one correspondence n <-> \(2^n\)
- …
Georg Cantor
- Born March 3, 1845 in St. Petersburg, Russia, died January 6, 1918 in Halle, Germany.
- Family moved to Germany when he was 12
- Completed his doctorate at the University of Berlin in 1867 under Weierstrass
- In 1874 he published a paper which fundamentally changed the way we think of infinity.
- Even Gauss had said, “I protest above all against the use of an infinite quantity as a completed one, which is mathematics is never allowed. The Infinite is only a manner of speaking” [quoted from ref:Dunham1991]

The integers are countable
- We can place the set of all integers (positive, negative, and zero) in one-to-one correspondence via the mapping: \[n \leftrightarrow \frac{1+(-1)^n(2n-1)}{4}\]
- (check examples)
- So they have the same cardinality (size of a set). He called this \(\aleph_0\)
The rational numbers are countable
- Draw the number array!
Reductio ad Absurdum
- A logical statement can only be true or false (it can’t be both).
- We assume the opposite of a statement (logical negation), and then through argumentation derive a logical contraction:
- Ex: “Assume that the square root of two is rational…. We proved that it is not rational.”
- It can’t be both rational and non-rational, and since our assumption (IS rational) was wrong, it must be that (NOT IS RATIONAL or irrational)
Cantor’s Diagonalization Theorem
- The interval of real numbers between 0 and 1 is not denumerable. (Cantor in his 1874 paper)
- Proof by contradiction – the reductio ad absurdum:
- Our assumption: Let’s assume that the interval IS denumerable and find this gives a contradiction.
- If the interval (0, 1) IS countable, what does that mean? There is a one-to-one correspondence with the set of natural numbers.
- Every number between 0 and 1 is on the right side of the table. …. I’ll draw the table in a moment
- To arrive at the contradiction, we will construct number that is not on the list.
- Do the proof… Blow some minds.
\(\infty \ge \infty\)?
- But the set of ALL real numbers is an infinite collection of all of these infinite, uncountable intervals. So surely it’s bigger…
- …Right?
- No.
- The cardinality of all real numbers is the same as the cardinality of the interval (0, 1):
- Consider the one-to-one correspondence:
- \(f(x) = \dfrac{2x-1}{x-x^2}\) from \((0,1) \to \mathbb{R}\).
Which is bigger? \(\mathbb{Q}\) or Irrationals?
- To answer the question formally, we need only one more theorem:
- Theorem: If B and C are denumerable (countable) sets and A is the set of all elements belonging to B or C or both, then A is also denumerable.
- (We can prove it, but we’ll go without proof… unless you want one)
- We know that if B and C are countable, then the union A = B U C is countable.
- So if the set of rationals and irrationals were the same size (countably infinite), then their union would be countable:
- {Real numbers} = {rationals} union {irrationals}
- But the set of real numbers is NOT countable.
- So the set of irrational numbers is also not countable!
Algebraic vs. Transcendental
- An algebraic number is one which is a solution to some polynomial with rational coefficients.
- A transcendental number is one that is not algebraic. We know \(\pi\), \(e\), and some others.
- Cantor didn’t.
- Lindemann wouldn’t prove \(\pi\) was transcendental for a decade!
- Cantor showed that the set of algebraic numbers is countable (a little beyond this class. If we had another class or two on the topic…)
- So all though the algebraic numbers (which include any conceivable roots of numbers) are nearly every number we can possibly imagine. And we can only imagine a handful of transcendentals
- There are vastly more transcendental numbers in the numeric universe!
Cantor does vastly more than this
- 1877 shows \(|(0,1) \times (0,1)| = |(0,1)|\)
- “I see it, but I don’t believe it.”
Is told to quit by respected colleague Mittag-Leffler: ref:laubenbacher1999
I am convinced that the publication of your new work… will greatly damage your reputation among mathematicians… but in this way, you will exercise no significant influence, which you naturally desire as does everyone who carries out scientific research.
- Quits mathematics
- Back to theology!
- Theologians love his work on infinite sets!
- 1895 publishes Beiträge zur Begründung der transfiniten Mengenlehre
- Discussing cardinalities of sets, showed that:
- \(|\mathcal{P}(A)| > |A|\) for any set \(A\). (Called “Cantor’s Theorem”)
- “In place of a given set L, another set M can be placed which is of greater power than L”
- … our term ’power sets’
- \(\aleph_0 < |(0,1)| < |\mathcal{P}((0,1))| < |\mathcal{P}(\mathcal{P}((0,1)))| < \dots\)
- an infinite chain of transfinite numbers
- … changed math forever
TODO Last Day
Summary/Wrap-up
What have we learned?
- What’s an interesting thing you learned?
- How might you use it in a classroom (or not)?
- How has your appreciation of math changed?
- Autumn
- Noha
- Abe
- Jacob
- Lizzie
- Amelia
What’s an interesting thing you learned? How might you use it in a classroom (or not)? How has your appreciation of math changed?
- John
- Isaac
- Sam
- Liz
- Quincy
- Tony
Brief Summary
- Content Areas:
- Numeration systems
- Symbols, place-value
- Different bases
- Base 10: Indians, Arabs, Chinese, Incans, basically the world now
- Base 20: Aztecs, Mayans*
- Base 60: Mesopotamians
- Algorithms for computations
- Existence or nonexistence of zero
- Early math in Egypt and Mesopotamia
- Practical problems in Egypt
- Papyri read like procedural textbooks
- Learning for its own sake in Mesopotamia
- Tablets of “scribal homework”
- Early quadratic formula
- Maybe early trig table
- Arguments against Plimpton (Eleanor Robson 2001)
- Arguments for (Mansfield 2017)
- Leading to Greek Mathematics
- Practical problems in Egypt
- Greek Math
- Geometry focus
- Numbers are line segments
- But basic number theory (studied in school) comes from this
- Major works (for school purposes)
- Euclid’s Elements
- Algebra in book II,
- All geometry through your high school and college
- Even 3D geometry of solids (“Non-Euclidean” Geometry)
- Euclid’s Elements
- Major works we talked about (for school purposes)
- Appolonius’ Conics
- Conic sections
- Eventually used to solve some cubic equations
- Structures we do in algebra
- Ptolemy’s Almagest
- Major contributer to early astronomy and so trig
- Euclid’s Elements
- Appolonius’ Conics
- Major works (for school purposes)
- Diophantus’ Arithmetica
- Gives us first symbolic algebra
- Something Hypatia builds on
- Keeps Fermat busy
- gives Euler something to do
- inspires Sophie Germain
- inspires Andrew Wiles
- Leads to in some sense a new area of math
- Diophantus’ Arithmetica
- Arab Math
- Preserves most things before
- Improves on everything before!
- Invent algebra closer to the form we know it.
- Al-Khwarizmi, Omar Khayyam, Thabit ibn Qurra, among others
- Algebra
- Italians did Math Battles
- Solution to the cubic
- Cardano and Tartaglia
- Cardano’s Ars Magna
- Cardano and Tartaglia
- Solution to the quartic
- Ferrari (using Cardano’s methods)
- Later algebra “abstract algebra” in France, Norway and modern day
- Calculations:
- Chord table of Hipparchus and Ptolemy
- Napier
- Logarithms
- Napier’s Bones
- Slide Rules (Oughtred)
- Pascal’s Pascaline
- Leibniz’s Stepped Reckoner
- Charles Babbage
- Difference Engine (actual) and
- Analytic Engine (hypothetic)
- Ada Lovelace on the Analytical engine
- Alan Turing, Bombe and theoretical machines
- Calculus
- Calculus before Newton and Leibniz
- Barrow, Gregory, Wallis, Fermat
- Newton and Leibniz
- Binomial Theorem
- Fundamental Theorem of Algebra for Partial Fractions Decomposition
- Series of the Bernoullis
- Euler
- Calculus before Newton and Leibniz
- Changes in the late 19th Century
- Non-Euclidean Geometry
- Bolyai, Lobachevsky, Gauss, Riemann, Poincare and others
- Rigorizing calculus
- Riemann, Cauchy, Weierstrauss
- Non-Euclidean Geometry
- Cantor and infinity
(Even then it wasn’t accepted!)
Is told to quit by respected colleague Mittag-Leffler: (Laubenbacher & Pengelley, 1999)
I am convinced that the publication of your new work… will greatly damage your reputation among mathematicians… but in this way, you will exercise no significant influence, which you naturally desire as does everyone who carries out scientific research.
- … and he does quit! Returns to theology
- Genie’s out of the bottle.
- Numeration systems
- A major take away:
- Math is created by people and people are people (brief, amusing list from (Martínez, 2012))
- Geometry changed in part with Lobachevsky, “a lousy student who became a teacher”
- “An alcoholic mathematician with marital problems, Hamilton, managed to break some rules of algebra by proposing new imaginary numbers.”
- “… a shy, unemployed high school dropout … Heaviside, managed to formulate a new algebra of vectors by breaking the usual rules of multiplication.”
- Abstract algebra was invented by the political revolutionary, Galois
- Serious people thought that Pythagoras was the Son of the god Apollo
- Gauss…
- and of course, a French lawyer from a quiet town with a lot of spare time.
- People knew a lot of things long ago
- The world is round
- Hydraulics and engineering are things Greeks and Arabs did
- including steam engines
- But some things took a long time to come around
- square roots are okay
- zero
- negative numbers aren’t scary
- women can do math
- But math is always changing. An example of just numbers
Originally only needed natural numbers (Kronecker quote)
God created the natural numbers; everything else is man’s handiwork.
- Eventually we needed zero
- Something less than zero?
- Eventually we need fractions
- But square roots are fine (irrationals)
- What if we think about square roots of negatives?
- Is there something smaller than any real number but still isn’t zero? (infinitessimals)
- Even more imaginary imaginary? (quaternians)
- Is there something more infinite that infinite?
- Math is created by people and people are people (brief, amusing list from (Martínez, 2012))
The Three Classical Problems
- Three Classical Problems:
Using only the tools of the compass and an unmarked straight-edge
- Trisection of an arbitrary angle
- Squaring the circle
- Duplication of the cube
- Are these theoretically important?
- No.
- There were no theorems that depended on their truth.
- … but attempts to solve them led to advancements.
- No.
- Can it be done?
- Trisection of the angle:
- For some angles, sure.
- If I use other tools? Sure.
- with a compass and straight-edge? No
- Proved in 1837 by Wantzel
- Requires “abstract algebra”
- Duplicating the cube
- Also no.
- 1837 (same person - same work)
- Squaring the circle
- No.
- Proved in 1882 by Lindemann
- He showed \(\pi\) is transcendental
- (transcendental numbers can’t be constructed. More abstract algebra)
- No.
- Trisection of the angle:
- The problems led to:
- Studying conic sections
- Solving cubic equations
- Duplicating the cube (e.g. \(x^3 = 2\))
- Trisection of angle (\(8x^3 - 6x -1 = 0\))
- (I have an example of this specific one below)
- Developing abstract algebra
- Constructable numbers
- Field extensions
- Here’s an example of a simple angle: \(60^\circ\):
The question:
- “Show that \(8x^3 - 6x -1 = 0\) has no rational solution”
- is asking, “can I construct \(20^\circ\)?”
- \(\cos 60^\circ = 1/2\)
- \(\cos (20^\circ + 20^\circ + 20^\circ) = 1/2\)
- \(4 \cos^3 (20^\circ) - 3\cos(20^\circ ) = 1/2\)
- Let \(x=\cos 20^\circ\)
- \(4x^3 - 3x = 1/2\)
- \(8x^3 - 6x -1 = 0\)
- this has no rational solution. So, no, I can’t construct it.
- The vagueness of the parallel postulate
- Led to a lot of people trying to prove or disprove it
- Big names:
- Ptolemy, Proclus
- Omar Khayyam, Nasir al-Din al-Tusi
- Johann Lambert
- (Lambert is the one who proved \(\pi\) is irrational)
- Carl Friedrich Gauss, Nokolai Lobachevsky, Janos Bolyai, Henri Poincare
- Leads to the necessarily geometric tools for Albert Einstein’s General Relativity
Modern Times
- Hilbert’s Problems
- In 1900, David Hilbert posed 23 problems at the International Congress of Mathematicians
- Various problems, for example,
- The continuum hypothesis (anything between counting numbers and the set of real numbers?)
- The Riemann Hypothesis
- … others
- Many solved, from 1900, 1920’s, 1930’s, 1950’s, 1960’s 1970’s,
1990’s.
- One was too vague, dismissed
- 4 unresolved
- 8 partially solved
- 10 solved
- Spurred development in many, many areas of math.
- The Millennium Problems
- Seven problems posed in 2000 by the Clay Mathematics Institute
- Solved (one):
- Poincare conjecture (solved in 2006 by Grigori Perelman)
- Won the Fields Medal, but declined it
- Poincare conjecture (solved in 2006 by Grigori Perelman)
- 6 Unsolved:
- The Riemann Hypothesis
- P vs. NP
- …
This might not be you. And that’s okay
- You might not be a super math nerd.
- I’m not
Maybe one of your students?
Future teachers of America!
- famous (and not famous) mathematicians were once kids
- share your enthusiasm
- Let’s inspire people
- And let’s have fun.
Future engineers of America!
- You can share your love of math, too!
- And please make bridges and buildings and electrical systems safe.
It’s been a great semester with all!
- Thanks for your insight and your passion.
- Keep doing great work, and good luck in your future!
- Thanks for a fun class.
Citations
Footnotes:
Randall Munroe, xkcd https://xkcd.com/2637/
By Manco Capac [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons
By Fedekuki (Own work) [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons
1988 James R. Newman, World of Mathematics, Volume 1, Tempus Books of Microsoft Press
CC-NC-SA by the British Museum
By Paul James Cowie (Pjamescowie) [Public domain], via Wikimedia Commons
Hind/Hindustan, Wikipedia, https://en.wikipedia.org/wiki/Names_for_India#Hind_.2F_Hindustan
Unicode symbols copied from Wikipedia contributors. (2022, May 16). Eastern Arabic numerals. In Wikipedia, The Free Encyclopedia. Retrieved 16:47, July 4, 2022, from https://en.wikipedia.org/w/index.php?title=Eastern_Arabic_numerals&oldid=1088218105
“Plimpton 322” by photo author unknown - image copied from http://www.math.ubc.ca/~cass/courses/m446-03/pl322/pl322.html. Licensed under Public domain via Wikimedia Commons
… actually “friendly” is attributed to Pythagoras according to Iamblicus
By Timrem [Public domain], from Wikimedia Commons
Greek Numerals 
//www.maa.org/press/periodicals/convergence/logarithms-the-early-history-of-a-familiar-function-john-napier-introduces-logarithms
YBC 7289 - Photo by Bill Casselman http://www.math.ubc.ca/~cass/Euclid/ybc/ybc.html from the Yale Babylonian Collection.
By Chris Rywalt - POVRay, Public Domain, https://commons.wikimedia.org/w/index.php?curid=1509454
By Justin Kunimune - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=65694588
By (derivative of) en: , CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=1731697
, CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=1731697